1772 résultats trouvés
Revenir à la recherche avancée
S=1+\sum_{k=1}^{2001}a_k ou a_{k+1}\neq a_{k}\in\{1,2,3,4\} si on prend b_k=a_{2k-1}+a_{2k}\in \{3,4,5,6,7\} S=1+X+\sum_{k=1}^{1000}b_k ou X=a_{2000}\in\{1,2,3,4\} on n'a plus l'obligation d'avoir b_{k+1}\neq b_{k} donc H=\sum_{k=1}^{k=1000}b_k peut prendre toutes les valeur entre 1000 x 3=3000 et ...
- 28 Aoû 2012, 07:34
- Forum: ⚔ Défis et énigmes
- Sujet: Oa 2001
- Réponses: 8
- Vues: 1136
Joker62 a écrit:Aviateurpilot de retour?
- 05 Aoû 2012, 23:07
- Forum: ⚔ Défis et énigmes
- Sujet: olympiades de mathématiques
- Réponses: 7
- Vues: 1814
m et n deux entiers strictement supérieurs à 1 qui vérifient : 1!3!5!.....................(2n-1)! = m! trouver ces deux entiers. MERCI mn^2-n+2 qui donne n\le 4 et m\le 4 donc (n,m)\in \{(1,1),(2,3)\} REMARQUE: V_2(X!)=max\{h\ tel\ que\ 2^h|X!\} et on peut facilement montrer que V_2(X!&...
- 05 Aoû 2012, 11:40
- Forum: ⚔ Défis et énigmes
- Sujet: olympiades de mathématiques
- Réponses: 7
- Vues: 1814
barbu23 a écrit:Bonjour à tous : :happy3:
Soit:
Je cherche un exemple de fonctions :verifiant :
Merci d'avance ! :happy3:
- 13 Mar 2009, 22:46
- Forum: ✯✎ Supérieur
- Sujet: Fonction inconnue !
- Réponses: 11
- Vues: 880
si on prend h(x)=f(x)+b^x et g(x)=3^{b^{x}+f(x)-1} alors h(x+y)=h(x)g(y)=h(y)g(x) on aura h(x)/g(x)=h(y)/g(y)=constance =c donc f(x)+b^x=c.3^{b^x+f(x)-1} pour un certain c constant...
- 05 Jan 2009, 19:43
- Forum: ⚔ Défis et énigmes
- Sujet: Equations fonctionelles
- Réponses: 4
- Vues: 866
Désolé lapras, j'avais oublié...mais au moins, là, la question est éclaircie... Allez, il reste toujours la deuxième, et là, promis, je ne dit rien de rien. motus. P_{2n+1}(-2n-3)=\sum_{k=0}^{n}\frac{(2n+3)^{2k}}{2k!}(1-\frac{2n+3}{2k+1}) [TEX]a_{2n+1}>-2n-3 et donc P_{2(...
- 31 Aoû 2008, 15:55
- Forum: ⚔ Défis et énigmes
- Sujet: Racines d'un polynôme
- Réponses: 14
- Vues: 1812
soit E ev de dim fini, et f:E\to E tel que f(famille libre)=famille libre. si f(x)=f(y) pour x,y\in E alors f(x-y)=0 . si x-y\neq 0 on prend z tel que la famille (z,x-y) libre on a donc (0,z)=(f(x-y),f(z)) libre , absurde donc x-y=0 ===...
- 03 Aoû 2008, 14:42
- Forum: ✯✎ Supérieur
- Sujet: Injectivité
- Réponses: 2
- Vues: 869
ce probleme est deja posté dans http://www.maths-forum.com/showthread.php?p=88961#post88961 [...] soit n de Z telque n\equiv r [6] il existe une infinite de x tel que x^3\equiv r [6] donc il existe une infinité de k tel que n=x^3+6k et on a 6k=(-k)^3+(-k)^3+(k+1)^3+(k-1&#...
- 03 Aoû 2008, 14:27
- Forum: ⚔ Défis et énigmes
- Sujet: Prouvez que ..
- Réponses: 32
- Vues: 2677
Help a écrit:[....]
2) supprimer des 0 revenant à diviser par 2 et 5 ne vas pas non plus le faire disparaitre.
[.....]
par exemple on peux passe de 101 à 11
mais là on a pas divisé par 2 ou 5 !!
- 25 Juil 2008, 16:08
- Forum: ⚔ Défis et énigmes
- Sujet: Les entiers rénovés
- Réponses: 12
- Vues: 1158
j'ai pas compris ce que tu veux dire par "rénové"??
par exemple pour n quelconque:
a)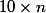
b) on supprime les 0 de 10n. et on trouve m=n sans zéro !!
c) 4m
là on peux dire que n est rénové??
par exemple pour n quelconque:
a)
b) on supprime les 0 de 10n. et on trouve m=n sans zéro !!
c) 4m
là on peux dire que n est rénové??
- 25 Juil 2008, 14:04
- Forum: ⚔ Défis et énigmes
- Sujet: Les entiers rénovés
- Réponses: 12
- Vues: 1158
on prend g(x)=(a,b) ssi x=a^{2}+b et b\in\{0,1,2,...,2a\} soit m tel que g(m)=(h,k) 1) si k=0 alors m est un carré. 2) si k=h+1 alors f(m)=(h+1)^2 est un carré 3) si k\in\{1,2,...,h\} alors g(f^{2}(m))=(h+1,k-1) et donc facileme...
- 25 Juil 2008, 13:54
- Forum: ⚔ Défis et énigmes
- Sujet: Carré d'un entier
- Réponses: 1
- Vues: 1101
3)a) \theta=a soit V_n=]-1/n,1/n[ on suppose que \forall n\in\mathbb{N}^*,\exists x_n\neq 0:\ x_n\in V_n\cap G_a on a x_n\to 0 et x_n\neq 0 et on a \forall n:\ x_n\mathbb{Z}\subset G_a ==> G_a\ dense\ dans\ \mathbb{R} mant pour x\in S_1 on prend y\in \mathbb{R};(y_n)\in G_a tel que y_n\to y ...
- 24 Juil 2008, 01:06
- Forum: ✯✎ Supérieur
- Sujet: Valeurs d'adhérences
- Réponses: 21
- Vues: 2160
jomanaomar a écrit:Bonjour tout le monde
le nombre 0.333333333..... = 1/3 et devient de la division 1/3
on a 0,9999999999...... = 1
je n'arrive pas trouver une opération (division) comme l'exemple précédent
merci
avant meme d'ecrire 0,999......
coment t'a pu montré que
- 20 Juil 2008, 00:43
- Forum: ✎✎ Lycée
- Sujet: Décimal périodique
- Réponses: 4
- Vues: 1287
Clise a écrit:tu as compris ce que représentait w déja ? et ce qu'est un nombre ordinal ?
no, car ans wikipedia, il y a une explication qui utilise des notions que je ne connais pas
- 17 Juil 2008, 19:12
- Forum: ✯✎ Supérieur
- Sujet: construction d'une bijection entre w^w et N
- Réponses: 12
- Vues: 1637
mais je ne conprend tjrs pas, c'est quoi w^w ete cett histoire d'ordinaux, lol
j'ai vu lien de wikipedia, mais j'ai rien compris :marteau:
j'ai vu lien de wikipedia, mais j'ai rien compris :marteau:
- 17 Juil 2008, 17:44
- Forum: ✯✎ Supérieur
- Sujet: construction d'une bijection entre w^w et N
- Réponses: 12
- Vues: 1637
j'ai été plus rapide mais Aaviateurpilot (que je salue) a fait plus simple :zen: moi, tous mes exposants sont différents. Par ailleurs, la méthode n'est malheurement pas implémentable vû l'extrême difficulté de factoriser un grand entier. salut mathelot, j'ai rien fait, c'est toi qui m'a guider ver...
- 17 Juil 2008, 17:32
- Forum: ✯✎ Supérieur
- Sujet: construction d'une bijection entre w^w et N
- Réponses: 12
- Vues: 1637
on prend p_i=i- eme nombre premier p_1=2,p_2=3,p_3=5... on prend la fonction tel que f((a_1,....,a_n,0,0,0...))=\bigprod_{i=1}^{n}p_i^{a_i} f est bien bijective. en effet, \forall n\in\mathbb{N} on peux ecrire n=\prod_{i=1}^{m}p_i^{c_i} avec c_i\ unique\(depend\ de\ n)\in \ma...
- 17 Juil 2008, 17:13
- Forum: ✯✎ Supérieur
- Sujet: construction d'une bijection entre w^w et N
- Réponses: 12
- Vues: 1637
[quote="Clise"] [....] ce qui implique que f(0)1[/TEX] pourquoi pas? mais je n'ai pas compris ce que tu veux dire par les w !!! mais je vais te donner un exemple qui resemble a ce w, il exemple pour S tel que N\subset S et pour un certain element X\in S on a X\ge n pour tt n\in N on prend ...
- 15 Juil 2008, 19:08
- Forum: ✯✎ Supérieur
- Sujet: fonction injective et ensemble bien ordonné
- Réponses: 33
- Vues: 2778
excusez moi mais je n'ai absolument pas compris :$ sinon aviateurpilot la puissance d'un ensemble est équivalente a son cardinal, c'est juste une autre appellation. Lierre Aeripz a ecris f(x)=\bigsum_{y\le x}2^{-a(x)} qui est bien defini , en effet puisque S est denombrable alors po...
- 14 Juil 2008, 17:04
- Forum: ✯✎ Supérieur
- Sujet: fonction injective et ensemble bien ordonné
- Réponses: 33
- Vues: 2778
leon1789 a écrit::++:
...ou comment numériser un sous-ensemble de N ! :id:
l'ensemble
- 14 Juil 2008, 16:33
- Forum: ✯✎ Supérieur
- Sujet: fonction injective et ensemble bien ordonné
- Réponses: 33
- Vues: 2778
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
