Elles sont tirées des olympiades viêtnamiennes, donc difficiles !
i) Soit
ii) Déterminer toutes les fonctions R-> R vérifiant :
Equations fonctionelles
5 messages
- Page 1 sur 1
Equations fonctionelles
par Zweig » 04 Jan 2009, 23:19
Salut,
Elles sont tirées des olympiades viêtnamiennes, donc difficiles !
i) Soit
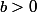
un réel donné. Déterminer toutes les fonctions R -> R vérifiant :
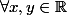
: =f(x)\cdot 3^{b^{y}+f(y)-1}+b^{x}\cdot\left(3^{b^{y}+f(y)-1}-b^{y}\right))
ii) Déterminer toutes les fonctions R-> R vérifiant : + f\left(4 + 3 \cdot \sqrt{2} \cdot x \right) = 2 \cdot f\left(\left(2 + \sqrt{2}\right) \cdot x\right))
Elles sont tirées des olympiades viêtnamiennes, donc difficiles !
i) Soit
ii) Déterminer toutes les fonctions R-> R vérifiant :
par Nightmare » 04 Jan 2009, 23:46
Ca ne sert pas à grand chose, autant se demander quelles sont les fonctions qui vérifient f(x+y)=f(x)+f(y) c'est intéressant, autant là, c'est à se détruire les neurones inutilement.
par ffpower » 04 Jan 2009, 23:57
chui dac aussi.Je me fiche de savoir si le résultat est interessant ou pas,mais au moins que l énoncé soit joli lol.Ca donne pas envie la
par aviateurpilot » 05 Jan 2009, 19:43
si on prend =f(x)+b^x)
et =3^{b^{x}+f(x)-1})
alors=h(x)g(y)=h(y)g(x))
on aura/g(x)=h(y)/g(y)=constance =c)
donc+b^x=c.3^{b^x+f(x)-1})
pour un certain c constant
le rest est facile, il fo seulement voir les solution de
alors
on aura
donc
le rest est facile, il fo seulement voir les solution de
5 messages
- Page 1 sur 1
Qui est en ligne
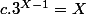
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :