Soit
Rappels :
Carré d'un entier
2 messages
- Page 1 sur 1
Carré d'un entier
par Zweig » 25 Juil 2008, 12:56
Salut,
Soit = n + \left\lfloor \sqrt{n}\right\rfloor)
. Montrer que pour tout entier naturel 
, la séquence , f^2(m), f^3(m)\ldots)
contient le carré d'un entier.
Rappels :
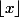
désigne la partie entière du réel 
, c'est-à-dire l'unique entier 
vérifiant : 
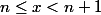
=\underbrace{ f\circ f\circ\cdots\circ f }_{n\, fois})
Soit
Rappels :
par aviateurpilot » 25 Juil 2008, 13:54
on prend =(a,b))
ssi 
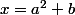
et 
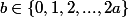
soit tel que =(h,k))
1) si
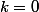
alors est un carré.
2) si
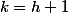
alors =(h+1)^2)
est un carré
3) si
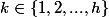
alors )=(h+1,k-1))
et donc facilement)=(h+k,0))
donc =(h+k)^{2})
4) si
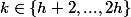
alors )=(h+1,k-1-h))
aved 
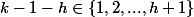
et on est maintenant dans le cas 3)
soit
1) si
2) si
3) si
et donc facilement
4) si
et on est maintenant dans le cas 3)
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :