Fonction inconnue !

par **barbu23** » 13 Mar 2009, 18:53

Bonjour à tous : :happy3:
Soit

:

Je cherche un exemple de fonctions :

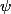
verifiant :

Merci d'avance ! :happy3:

par **uztop** » 13 Mar 2009, 19:05

Salut,

est ce qu'il faut que

dépende réellement des deux variables ?
Sinon,

est solution

par **barbu23** » 13 Mar 2009, 19:31

oui

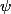
depend des deux variables

et

! C'est peut être le seul exemple qui exste à mon avis ! :hein:
Merc uztop ! :happy3:

par **nuage** » 13 Mar 2009, 21:16

Salut,
il y a aussi deux fonctions constantes qui conviennent :

et

par **Doraki** » 13 Mar 2009, 21:41

Il y a plein de fonctions qui peuvent marcher.

Quelles sont les fonctions f : R -> R, continues, telles que pour tout a,b,
f (a*b) = f(a)*f(b) ?

par **barbu23** » 13 Mar 2009, 22:32

Oui, mais jusqu'à maintenant, on laisse tomber la variable

qui est necessaire et dois figurer dans l'expression de

!:
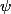
Par contre les fonctions qui verifient l'expression de Doraki sont les morphismes non ? :happy3:
Nuage trouve par contre toutes les

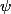
bilinéaires qi verifient la formule que j'ai donnée ! mais si on se place dans un espace plus large que les applications bilinéaires, à mon avis les

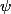
n'existent pas ! Il faudra pet essayer de le montrer ! mais pour le moment aucune idée ne me vient à l'esprit ! ce n'est pas vraiment assez facile ! :happy3:
Merci d'avance de vos reponses ! :happy2:

par **busard_des_roseaux** » 13 Mar 2009, 22:40

barbu23 a écrit:Bonjour à tous : :happy3:
Soit :

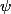
Je cherche un exemple de fonctions : verifiant :
Merci d'avance ! :happy3:

par **aviateurpilot** » 13 Mar 2009, 22:46

barbu23 a écrit:Bonjour à tous : :happy3:
Soit :

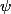
Je cherche un exemple de fonctions : verifiant :
Merci d'avance ! :happy3:

par **barbu23** » 13 Mar 2009, 23:43

Merci beaucoup busard de roseaux ! :happy3: c'est un très beau exemple ! je vais essayer de travailler avec ! merci encore une fis bour le bel exemple que tu viens nous fournir ! :happy3:
Amicalement ! :happy3:

par **Doraki** » 13 Mar 2009, 23:59

les fonctions f continues vérifiant f(ab)=f(a)f(b) sont les
f(a)= exp(x* ln(a)) pour a > 0
f(0)= 0
f(a)= +/- exp(x* ln(-a)) pour a < 0,
avec x > 0.

exp(x * ln|a|), c'est pas continu en (0,0), et il se passe des trucs horribles pour x<0.

mais on peut prendre psi(x,a) = exp(phi(x) * ln |a|) pour n'importe quelle fonction phi continue de R dans R+*.

et on peut aussi changer le signe de psi(x,a) pour a<0.

par **ffpower** » 14 Mar 2009, 00:03

pas tout a fait en fait.ya un prob de continuité en 0.Faut plutot prendre phi(a,x)=|a|^u(x) ou u est continue strictement positive(par ex u(x)=x²+1)....

tite remarque au passage:apparament,on peut par contre pas trouver de phi C-infinie

edit:doublé lol

par **barbu23** » 14 Mar 2009, 05:13

Merci beaucoup à vous tous pour toutes ces précisions ! :happy3:
J'ai un autre problème à vous soumettre :
On note par :

l'ensemble des couples de fonctions continues :
Soit

telle que :

et

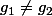
Pour que cette expression ait un sens, il faut et il suffit que :

Celà implique que :

avec :

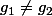
On ne peut pas déduire que :

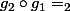
que si :

est injective par rapport à la deuxième variable ! ce qui n'est pas toujors le cas !
Je cherche un exemple de fonctions verifiant cette dernière expression ! c'est à dire :

avec :

..
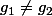
Merci infiniment ! :happy3:

Fonction inconnue !

Fonction inconnue !

Qui est en ligne