Prouvez que ..
Olympiades mathématiques, énigmes et défis
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 31 Juil 2008, 23:12
par _-Gaara-_ » 31 Juil 2008, 23:12
chaque entier peut être écrit comme la somme de 5 cubes parfaits ^^
Bon courage.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Aoû 2008, 02:12
par Zweig » 01 Aoû 2008, 02:12
Ton énoncé manque de précisions pour que l'exercice devienne difficile :
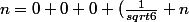^3 - (\frac{1}{sqrt{6}} - n)^3)
"Montrer que tout entier n s'écrit comme la somme de 5 cubes entiers non nuls"
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 01 Aoû 2008, 08:11
par nodgim » 01 Aoû 2008, 08:11
des cubes d'entiers?
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 01 Aoû 2008, 08:14
par nodgim » 01 Aoû 2008, 08:14
Ah oui, tu voulais dire "avec 5 cubes au maximum"!
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 01 Aoû 2008, 08:24
par nodgim » 01 Aoû 2008, 08:24
Et pour faire 6 ou 7 ? :triste:
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 01 Aoû 2008, 08:56
par nodgim » 01 Aoû 2008, 08:56
Et combien de cubes pour faire 114 ? :zen:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Aoû 2008, 09:11
par Imod » 01 Aoû 2008, 09:11
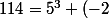^3+(-1)^3+(-1)^3+(-1)^3)
:we:
Imod
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Aoû 2008, 09:12
par Imod » 01 Aoû 2008, 09:12
nodgim a écrit:Ah oui, tu voulais dire "avec 5 cubes au maximum"!
En prenant les cubes de 0 on peut s'affranchir de cette subtilité !
Imod
-
john32
- Membre Relatif
- Messages: 239
- Enregistré le: 08 Juil 2008, 10:34
-
 par john32 » 01 Aoû 2008, 09:16
par john32 » 01 Aoû 2008, 09:16
Impressionant mais de la à la dire pour chaque entiers il doit ya avoir une démo à base d'égalités remarquables peut être !
Mais la je sais pas comment me lancer
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 01 Aoû 2008, 10:09
par acoustica » 01 Aoû 2008, 10:09
Je ne sais pas si ca peut avoir une quelconque utilite, mais j'ai trouve comment exprimer un entier pair en somme de 5 cubes de rationnels (parce que cube parfait, ca peut etre rationnel non?).
/k)^3+((k+1)/k)^3+((k+1)/k)^3+((-k-2)/k)^3+((k+1)/k)^3)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Aoû 2008, 10:15
par Zweig » 01 Aoû 2008, 10:15
_-Gaara-_ a écrit:chaque entier peut être écrit comme la somme de 5 cubes parfaits
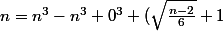^3 - (\sqrt{\frac{n-2}{6}}-1)^3)
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 01 Aoû 2008, 10:18
par acoustica » 01 Aoû 2008, 10:18
Zweig a écrit: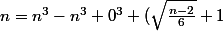^3 - (\sqrt{\frac{n-2}{6}}-1)^3)
Mais ca, ca revient a une somme de deux cubes non nuls et de 3 nuls, puisque il y en a deux qui s'annulent entre eux.
L'ideal serait de trouver une formule generale avec que des termes non nuls, et sans distinction de cas si possible (encore que ce ne soit pas vraiment un probleme)
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Aoû 2008, 10:18
par Zweig » 01 Aoû 2008, 10:18
Cela dit, j'avais inventé il y a quelques temps un exercice analogue :
Montrer qu'il existe une infinité de rationnels

, non cube parfait, tels que l'équation
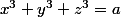
admette une infinité de solutions non nulles (x,y,z) Q^3
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 01 Aoû 2008, 10:19
par Zweig » 01 Aoû 2008, 10:19
acoustica a écrit:Mais ca, ca revient a une somme de deux cubes non nuls et de 3 nuls, puisque il y en a deux qui s'annulent entre eux.
L'ideal serait de trouver une formule generale avec que des termes non nuls, et sans distinction de cas si possible (encore que ce ne soit pas vraiment un probleme)
Désolé, mais tel que l'énoncé a été posé, ma solution convient : il n'a pas précisé "cubes d'entiers" et "cubes non nuls" :ptdr:
-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 01 Aoû 2008, 10:21
par acoustica » 01 Aoû 2008, 10:21
Zweig a écrit:Désolé, mais tel que l'énoncé a été posé, ma solution convient : il n'a pas précisé "cubes d'entiers" et "cubes non nuls" :ptdr:
Tout a fait.
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 01 Aoû 2008, 10:31
par _-Gaara-_ » 01 Aoû 2008, 10:31
Non mais vraiment .. lollllllllllllll
des cubes : entiers !
-
_-Gaara-_
- Membre Complexe
- Messages: 2813
- Enregistré le: 03 Nov 2007, 14:34
-
 par _-Gaara-_ » 01 Aoû 2008, 10:32
par _-Gaara-_ » 01 Aoû 2008, 10:32
Zweig a écrit:Désolé, mais tel que l'énoncé a été posé, ma solution convient : il n'a pas précisé "cubes d'entiers" et "cubes non nuls" :ptdr:
0 fait partie de l'ensemble des entiers -_____________________-
j'ai imposé aucune condition !!!!!!!!!!!
et Alexis vérifie ta boîte mail

-
acoustica
- Membre Irrationnel
- Messages: 1043
- Enregistré le: 08 Juil 2008, 10:00
-
 par acoustica » 01 Aoû 2008, 11:42
par acoustica » 01 Aoû 2008, 11:42
_-Gaara-_ a écrit:Alexis vérifie ta boîte mail

C'est fait

Si on doit faire le probleme avec des cubes entiers, c'est autrement plus difficile!
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 01 Aoû 2008, 12:34
par Clembou » 01 Aoû 2008, 12:34
_-Gaara-_ a écrit:0 fait partie de l'ensemble des entiers -_____________________-
j'ai imposé aucune condition !!!!!!!!!!!
et Alexis vérifie ta boîte mail

Et quand tu dis
somme, on ne veut pas de signe
- :++:
-
Ruch
- Membre Relatif
- Messages: 119
- Enregistré le: 17 Mar 2008, 00:42
-
 par Ruch » 01 Aoû 2008, 12:42
par Ruch » 01 Aoû 2008, 12:42
Moi j'ai juste démontrer que tout multiple de 6 peut s'écrire comme la somme de 5 cubes.
2*(-t)^3 + (t+1)^3 + (t-1)^3 = 6t. (le 5éme cube est nul).
Donc on devrait prouver que tout entier n peut s'écrire: k^3 + 6t
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
