salut
encore un énoncé et une rédaction médiocre ... (sauter des lignes, aérer, utiliser des espaces dans les formules ...)
qui est p ?
6927 résultats trouvés
Revenir à la recherche avancée
- 01 Nov 2017, 21:06
- Forum: ✯✎ Supérieur
- Sujet: Décomposition en éléments simples
- Réponses: 6
- Vues: 307
Re: Exercice de spécialité
quand on n'a pas la réponse à un endroit on va chercher ailleurs ... https://www.ilemaths.net/sujet-exercice ... 59353.html ... au lieu de réfléchir ...
- 01 Nov 2017, 20:58
- Forum: ✎✎ Lycée
- Sujet: Exercice de spécialité
- Réponses: 21
- Vues: 1762
Re: tribu
salut
la plus grande tribu sur un ensemble fini A est P(A) ... qui ne contient que des ensembles finis ...
leur complémentaire dans X sont évidemment infinis ... (si X l'est) ...
la plus grande tribu sur un ensemble fini A est P(A) ... qui ne contient que des ensembles finis ...
leur complémentaire dans X sont évidemment infinis ... (si X l'est) ...
- 31 Oct 2017, 20:28
- Forum: ✯✎ Supérieur
- Sujet: tribu
- Réponses: 11
- Vues: 352
Re: Analyse réel - Théorème de Convergence Monotone
ok merci ... oui fonctions étagées ... ce qui répond à toutes mes questions ...
- 30 Oct 2017, 19:35
- Forum: ✯✎ Supérieur
- Sujet: Analyse réel - Théorème de Convergence Monotone
- Réponses: 5
- Vues: 672
Re: Analyse réel - Théorème de Convergence Monotone
salut
1/ qu'est-ce qu'une fonction simple ?
2/ (et 3/) ne faut-il pas que phi soit mesurable ? (et alors phi_n le sera)
3/ pourquoi M existe-t-il ?
1/ qu'est-ce qu'une fonction simple ?
2/ (et 3/) ne faut-il pas que phi soit mesurable ? (et alors phi_n le sera)
3/ pourquoi M existe-t-il ?
- 30 Oct 2017, 19:11
- Forum: ✯✎ Supérieur
- Sujet: Analyse réel - Théorème de Convergence Monotone
- Réponses: 5
- Vues: 672
Re: Deduire un ensemble à partir d'une norme de vecteurs
salut
||3MG|| = 6 <=> MG = 2 et il suffit de retourner au collège pour reconnaitre ... ??
||3MG|| = 6 <=> MG = 2 et il suffit de retourner au collège pour reconnaitre ... ??
- 30 Oct 2017, 19:05
- Forum: ✎✎ Lycée
- Sujet: Deduire un ensemble à partir d'une norme de vecteurs
- Réponses: 2
- Vues: 428
Re: BIJECTIVITE
salut
l'équation f(x) = -1 a-t-elle des solutions ?
l'équation f(x) = -1 a-t-elle des solutions ?
- 30 Oct 2017, 19:04
- Forum: ✎✎ Lycée
- Sujet: BIJECTIVITE
- Réponses: 2
- Vues: 293
Re: topologie diamétre et adhérence
salut
et c'est quoi par définition le diamètre d'une partie d'un ensemble ?
REM : puisque A est inclus dans son adhérence A* on a évidemment d(A) =< d(A*) ...
et c'est quoi par définition le diamètre d'une partie d'un ensemble ?
REM : puisque A est inclus dans son adhérence A* on a évidemment d(A) =< d(A*) ...
- 29 Oct 2017, 20:07
- Forum: ✯✎ Supérieur
- Sujet: topologie diamétre et adhérence
- Réponses: 2
- Vues: 1402
Re: Enigme SD 2 : invalidation opératoire globale
Là où je comprend vraiment pas comment on a pu en arriver là au niveau de 'enseignement des maths., c'est de voir la quantités de personnes (SigmaDelta est loin d'être le seul) qui n'ont même pas compris qu'une fonction (par exemple la fonction puissance), c'est une "machine" où on rentre...
- 28 Oct 2017, 16:37
- Forum: ⚔ Défis et énigmes
- Sujet: Enigme SD 2 : invalidation opératoire globale
- Réponses: 35
- Vues: 905
Re: pourcentage d'erreur
développe ... au lieu de calculer la parenthèse ...
- 27 Oct 2017, 19:45
- Forum: ✎✎ Lycée
- Sujet: pourcentage d'erreur
- Réponses: 5
- Vues: 252
Re: pourcentage d'erreur
a = 1/0,35 = 20/7 et 2,85 = 57/20 et 2,86 = 143/50 (a - 2,85)/a = 7/20 * (20/7 - 57/20) = 1 - 399/400 = 1/400 = 0,0025 (2,86 - a)/a = 143/50 * 7/20 - 1 = 1001/1000 - 1 = 1/1000 = 0, 001 en choisissant 2,85 au lieu de 2,86 tu multiplies ton erreur par 2,5 ... mais bon de quoi...
- 27 Oct 2017, 18:26
- Forum: ✎✎ Lycée
- Sujet: pourcentage d'erreur
- Réponses: 5
- Vues: 252
Re: Nombre complexe
salut
/e^{-ia} = e^{ia}(e^{ia} + e^{-ia})e^{ia} = (e^{ia} + e^{-ia})e^{2ia})
or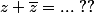
or
- 27 Oct 2017, 16:39
- Forum: ✯✎ Supérieur
- Sujet: Nombre complexe
- Réponses: 19
- Vues: 554
Re: Uniforme continuité
Bonjour le produit de deux variables n'est-il pas continue ? @zygomatique, tu veux dire uniformément continue.? J'ai tout de même un doute sur la continuité uniforme de sin(xy) pour en revenir au sinus : je pensais qu'en étant borné et à dérivée bornée cela serait suffisant ... avec la continuité ....
- 27 Oct 2017, 16:32
- Forum: ✯✎ Supérieur
- Sujet: Uniforme continuité
- Réponses: 11
- Vues: 510
Re: pourcentage d'erreur
salut
(valeur approchée - valeur exacte)/valeur exacte ... * 100 pour se ramener à un pourcentage ..
(valeur approchée - valeur exacte)/valeur exacte ... * 100 pour se ramener à un pourcentage ..
- 27 Oct 2017, 16:26
- Forum: ✎✎ Lycée
- Sujet: pourcentage d'erreur
- Réponses: 5
- Vues: 252
Re: Bijection réciproque d'isomorphisme d'anneau
ben quel manque de tact ?
- 27 Oct 2017, 09:29
- Forum: ✯✎ Supérieur
- Sujet: Bijection réciproque d'isomorphisme d'anneau
- Réponses: 4
- Vues: 801
Re: Bijection réciproque d'isomorphisme d'anneau
salut ben on vérifie les conditions de la définition de morphisme d'anneau en notant g l'inverse de f si x et y sont dans A alors f(x + y) = f(x) + f(y) donc en composant par g : x + y = g[f(x) + f(y)] (*) maintenant en écrivant X = f(x) et Y = f(y) alors (*) <=> g(X + Y) = x + y = g(X) + g(Y) et on...
- 26 Oct 2017, 19:32
- Forum: ✯✎ Supérieur
- Sujet: Bijection réciproque d'isomorphisme d'anneau
- Réponses: 4
- Vues: 801
Re: Uniforme continuité
merci ...
- 26 Oct 2017, 19:14
- Forum: ✯✎ Supérieur
- Sujet: Uniforme continuité
- Réponses: 11
- Vues: 510
- 26 Oct 2017, 19:08
- Forum: ✎✎ Lycée
- Sujet: Création d'un algorithme grâce à une formule de récurrence
- Réponses: 27
- Vues: 2235
Re: Fonction lipschitzienne
salut
c'est pas clair ... et on n'a pas d'énoncé ...
c'est pas clair ... et on n'a pas d'énoncé ...
- 22 Oct 2017, 18:35
- Forum: ✯✎ Supérieur
- Sujet: Fonction lipschitzienne
- Réponses: 4
- Vues: 284
Re: Uniforme continuité
salut
la fonction sin n'est-elle pas uniformément continue ?
le produit de deux variables n'est-il pas continue ?
peut-être utiliser les hypothèses ...
la fonction sin n'est-elle pas uniformément continue ?
le produit de deux variables n'est-il pas continue ?
peut-être utiliser les hypothèses ...
- 22 Oct 2017, 18:32
- Forum: ✯✎ Supérieur
- Sujet: Uniforme continuité
- Réponses: 11
- Vues: 510
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
