Khôlle : Nombres complexes
43 messages
- Page 2 sur 3 - 1, 2, 3
points du cercle à coordonnées rationnelles
re,
l'exo de NightMare est bien intéressant :++: et donne l'envie de gloser un peu... :id:
Prop1
si u,v,m,n sont entiers naturels , les fractions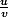
et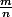 sont irréductibles alors
sont irréductibles alors
^2+({m \over n})^2=1)
entraine que v et n ont exactement les mêmes diviseurs
et sont donc des entiers naturels égaux.
Les points rationnels du cercle sont de la forme
^2+({ y \over z})^2=1)
et donc (x,y,z) forme un triplet pythagoricien
exemple: (3;4;5)
Prop2
les triplets pythagoriciens (x,y,z) sont complètement décrits ici
les triplets pythagoriciens primitifs vérifient
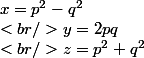
Ils forment un sous-groupe multiplicatif de matrices de rotations
dont la multiplication est décrite par
^2-(p_1q+pq_1)^2 \over (pp_1-qq_1)^2+(p_1q+pq_1)^2} & & { - 2(pp_1-qq_1)(p_1q+pq_1) \over (pp_1-qq_1)^2+(p_1q+pq_1)^2} \\<br />{2(pp_1-qq_1)(p_1q+pq_1) \over ((pp_1-qq_1)^2+(p_1q+pq_1)^2} & & {(pp_1-qq_1)^2-(p_1q+pq_1)^2 \over (pp_1-qq_1)^2+(p_1q+pq_1)^2} \\<br />\end{pmatrix})
Prop3
Comme les triplets pythagoriciens (x,y,z) primitifs vérifient
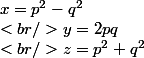
on remarque que , en posant
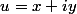
alors
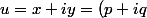^2)
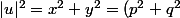^2)
et donc que les points du cercle à coordonnées rationnelles
s'écrivent
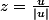 où
où  est le carré d'un nombre complexe à coordonnées entières
est le carré d'un nombre complexe à coordonnées entières 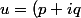^2)
exemple:
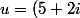^2) (au pif)
(au pif)
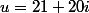
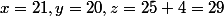
) est bien un triplet pythagoricien
est bien un triplet pythagoricien
conclusion provisoire
l'existence de points du cercle à coordonnées rationnelles
semble avoir un lien avec l'élévation au carré et donc au
doublement de l'arc)
ou de l'angle polaire, comme on voudra
je pense que la réciproque est valide.:
ces points à coord. rationnelles , sur le cercle, proviennent de carrés de points du plan complexe à coordonnées entières p+iq ,de tangente ou cotangente
rationnelles= {p \over q}) ou
ou 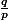 ,
,
tangente ou cotangente de leur angle polaire.
En élevant au carré, et en divisant par le module,
on double l'arc en) et
et )
pour obtenir un point rationnel du cercle.
évidemment, ces points "projectifs" (un point d'un espace projectif=
une droite du plan passant par l'origine) entiers ont un intérêt arithmétique...:
l'exo de NightMare est bien intéressant :++: et donne l'envie de gloser un peu... :id:
Prop1
si u,v,m,n sont entiers naturels , les fractions
et
entraine que v et n ont exactement les mêmes diviseurs
et sont donc des entiers naturels égaux.
Les points rationnels du cercle sont de la forme
et donc (x,y,z) forme un triplet pythagoricien
exemple: (3;4;5)
Prop2
les triplets pythagoriciens (x,y,z) sont complètement décrits ici
les triplets pythagoriciens primitifs vérifient
Ils forment un sous-groupe multiplicatif de matrices de rotations
dont la multiplication est décrite par
Prop3
Comme les triplets pythagoriciens (x,y,z) primitifs vérifient
on remarque que , en posant
alors
et donc que les points du cercle à coordonnées rationnelles
s'écrivent
exemple:
conclusion provisoire
l'existence de points du cercle à coordonnées rationnelles
semble avoir un lien avec l'élévation au carré et donc au
doublement de l'arc
ou de l'angle polaire, comme on voudra
je pense que la réciproque est valide.:
ces points à coord. rationnelles , sur le cercle, proviennent de carrés de points du plan complexe à coordonnées entières p+iq ,de tangente ou cotangente
rationnelles
tangente ou cotangente de leur angle polaire.
En élevant au carré, et en divisant par le module,
on double l'arc en
pour obtenir un point rationnel du cercle.
évidemment, ces points "projectifs" (un point d'un espace projectif=
une droite du plan passant par l'origine) entiers ont un intérêt arithmétique...:
II.b
re NightMare,
je serai intéressé par le quotient de E par F :we:
peux-tu m'expliquer ce dont il s'agit (algèbre+géométrie) ?
je serai intéressé par le quotient de E par F :we:
peux-tu m'expliquer ce dont il s'agit (algèbre+géométrie) ?
Salut,
J'ai des gros soucis sur cet exo, j'avance vraiment pas, même avec l'indice.
Déjà j'identifie le plan au plan complexe et donc on a pour x dans [0,1] x+ix² dans notre partie du plan (qui est un groupe)
Donc il "suffit" de ùontrer que R et iR sont dans ce groupe pour pouvoir dire que ce groupe est en fait C.
Comment continuer ?
Merci !!
J'ai des gros soucis sur cet exo, j'avance vraiment pas, même avec l'indice.
Déjà j'identifie le plan au plan complexe et donc on a pour x dans [0,1] x+ix² dans notre partie du plan (qui est un groupe)
Donc il "suffit" de ùontrer que R et iR sont dans ce groupe pour pouvoir dire que ce groupe est en fait C.
Comment continuer ?
Merci !!
Bon, je te donne le début "complet" :
- Comme P et stable par soustraction et que (0,0)=(0,0²) est dans P, l'opposé de tout élément de P est encore dans P et donc P est aussi stable par addition : c'est bien un groupe additif.
- Pour tout x de [0,1/2], (x,x²) est dans P donc (2x,2x²)=(x,x²)+(x,x²) aussi.
mais 2x est dans [0,1] donc (2x,4x²)=(2x,(2x)²) est lui aussi dans P.
On en déduit que (0,2x²)=(2x,4x²)-(2x,2x²) est dans P pour tout x de [0,1/2], ce qui signifie (0,y) est dans P pour tout y de [0,1/2].
- Comme P et stable par soustraction et que (0,0)=(0,0²) est dans P, l'opposé de tout élément de P est encore dans P et donc P est aussi stable par addition : c'est bien un groupe additif.
- Pour tout x de [0,1/2], (x,x²) est dans P donc (2x,2x²)=(x,x²)+(x,x²) aussi.
mais 2x est dans [0,1] donc (2x,4x²)=(2x,(2x)²) est lui aussi dans P.
On en déduit que (0,2x²)=(2x,4x²)-(2x,2x²) est dans P pour tout x de [0,1/2], ce qui signifie (0,y) est dans P pour tout y de [0,1/2].
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour le groupe j'avais bon, mais j'avoue que j'ai même pas penser a soustraire les deux machins que t'avais calculer ....
donc comme P est un groupe il vient assez rapidement que iR est incus dans P, de plus (x,x²) et (0,y) sont dans P pour x et y de[0,1/2] en prenant y=x² il vient que (x,0) pour tout x de [0,1/2] est dans P , donc R entier, donc C entier , ainsi P est le plan complexe tout entier. C'est dans le genre ?
donc comme P est un groupe il vient assez rapidement que iR est incus dans P, de plus (x,x²) et (0,y) sont dans P pour x et y de[0,1/2] en prenant y=x² il vient que (x,0) pour tout x de [0,1/2] est dans P , donc R entier, donc C entier , ainsi P est le plan complexe tout entier. C'est dans le genre ?
43 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
