Khôlle : Un brin de groupe dans Lagrange.

[benekire2]

J'ai l'impression que "ça rame" principalement du fait que Nightmare est parti à faire une preuve par l'absurde et pas Benekire.... (doù difficultés à se comprendre...)

reste encore a savoir ce que tu appelle le début de preuve de benekire ...

Mon idée , qui n'est surement pas la bonne , est de trouver un ensmebl de cardinal H disjoint de H ...

[benekire2]

Je déterre le topic !

Je me souviens dans un autre topic que tu m'avais demander si je savais démontrer la formule des combinaisons, et tu avais précisé qu'il y avait une méthode et une autre qui passe par les classes d'équivalences.

Est-ce que l'on pourrait m'éclairer sur ces deux démonstrations s'il vous plait ? Merci beaucoup !

[Ben314]

Pour répondre à ton M.P., si tu veut définir les vecteurs à l'aide des classes d'équivalences, tu considère l'ensemble des bipoints (A,B) du plan (ou de l'espace) ainsi que la relation dite "d'équipolence" suivante :
(A,B) R (A',B') lorsque [AB'] et [BA'] ont même millieu (i.e. ABB'A' est un parallélogramme à la rigueur dégénéré).
On montre que R est bien une relation d'équivalence (réflexive, symétrique et transitive) et ce sont les classes d'équivalence que l'on appelle vecteur.
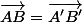
En fait est la classe du bipoint (A,B) et, par définition, on a ssi [AB'] et [BA'] ont même millieu.

Concernant les combinaisons, je suis pas sûr de voir de quoi parlait Nightmare.
Peut être voulait il dire que si on considère sur l'ensemble des n! permutations de {1..n} la relation "avoir les mêmes p premiers éléments", c'est une relation d'équivalence et toutes les classe d'équivalence ont p!x(n-p)! éléments (nbre de façon de ranger les p premiers et les n-p derniers) donc le nombre de classes est n!/(p!x(n-p)!)

[benekire2]

Merci beaucoup pour cette réponse qui m'éclaire pas mal !!
Pour les vecteurs, c'est une définition simple, mais qui a le mérite d'être concise !
Pour les combinaisons, ça concerne ben la formule , je vais chercher encore un peu pour celle ci ,

En tout cas merci :id:

[Nightmare]

Concernant les combinaisons, je suis pas sûr de voir de quoi parlait Nightmare.
Peut être voulait il dire que si on considère sur l'ensemble des n! permutations de {1..n} la relation "avoir les mêmes p premiers éléments", c'est une relation d'équivalence et toutes les classe d'équivalence ont p!x(n-p)! éléments (nbre de façon de ranger les p premiers et les n-p derniers) donc le nombre de classes est n!/(p!x(n-p)!)

C'était bien ce que j'avais en tête !

[benekire2]

ok merci beaucoup a vous deux, je vais relire le message de ben plus en profondeur !