Khôlle : Exponentielle et équadiff
80 messages
- Page 3 sur 4 - 1, 2, 3, 4
par Nightmare » 24 Mar 2010, 13:05
C'est l'idée. Essaye de faire le III] qui est du même ordre et est un bon entrainement.
par benekire2 » 24 Mar 2010, 18:24
De retour de la JAPD !!
Le problème pour le III ça va être de voir comment appliquer les accroissements finis. Je suis entrain d'y réfléchir.
Le problème pour le III ça va être de voir comment appliquer les accroissements finis. Je suis entrain d'y réfléchir.
par benekire2 » 25 Mar 2010, 18:09
Bon pour la III je vais m'y mettre, en fait sylviel m'a pas mal aidé hier.
Donc pour tout epsilon il existe X tel que x>X => |e^-xf(x)-1|
On prend X+1 et on applique le TAF entre X et X+1 donc on a l'existence d'un c tel que:
-2epsilon
or -epsilon<-e^-cf(c)
donc -epsilon
Après que faire ? Déjà c'est la bonne voie ?
Donc pour tout epsilon il existe X tel que x>X => |e^-xf(x)-1|
On prend X+1 et on applique le TAF entre X et X+1 donc on a l'existence d'un c tel que:
-2epsilon
or -epsilon<-e^-cf(c)
donc -epsilon
Après que faire ? Déjà c'est la bonne voie ?
par Nightmare » 25 Mar 2010, 19:55
Sans vérifier les calculs, le premier problème est qu'avoir un encadrement de exp(-c)f'(c) n'est pas trop utile car c est fixé, même s'il dépend de x. Ce qu'il nous faudrait, c'est un encadrement de exp(-x)f'(x) pour tout x (du moins assez grand).
Pour commencer, on peut écrire que=e^{x}(1+\epsilon(x)))
avec 
une fonction, dérivable (!), qui tend vers 0 en +oo.
Du coup=1+\epsilon(x)+\epsilon'(x))
. C'est ce terme à droite qui nous intéresse. Tu pourrais donc par exemple appliquer le TAF à . Ne pas oublier aussi que f est convexe !
Pour commencer, on peut écrire que
Du coup
par Sylviel » 25 Mar 2010, 21:06
Non, à la fin c'est 3 epsilon et non pas epsilon...
Pour défendre mon idée je pensais m'en sortir ensuite par l'hypothèse de croissance sur f', mais à la reflexion c'est moins évident que je ne l'aurai cru. Du coup je laisse tomber ma piste.
Pour défendre mon idée je pensais m'en sortir ensuite par l'hypothèse de croissance sur f', mais à la reflexion c'est moins évident que je ne l'aurai cru. Du coup je laisse tomber ma piste.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
par benekire2 » 26 Mar 2010, 12:21
donc il suffit ( c'est un grand mot !! ) de montrer que )
converge vers 0.
Mais quand je vais appliquer le TAF, là aussi on ne va avoir qu'un seul point ... ça va être problématique.
comme)
converge vers 0, pour tout k il existe A tel que x>A => -k<e(x)<k
en appliquant le TAF sur A et A+1 il existe c tel que -2k<e'(c)<2k
Voilà ... c'est comme ça que tu voulais que j'applique le TAF ?
Mais quand je vais appliquer le TAF, là aussi on ne va avoir qu'un seul point ... ça va être problématique.
comme
en appliquant le TAF sur A et A+1 il existe c tel que -2k<e'(c)<2k
Voilà ... c'est comme ça que tu voulais que j'applique le TAF ?
par benekire2 » 26 Mar 2010, 13:35
c'est à dire ??
Moi ma version c'est :
il existe c entre a et b tel qu f'(c)=(f(b)-f(a))/b-a
Moi ma version c'est :
il existe c entre a et b tel qu f'(c)=(f(b)-f(a))/b-a
par Nightmare » 26 Mar 2010, 13:45
Une "variante" intéressante, qui est bien entendu strictement équivalente, est de considérer non plus un c dans ]a,b[ mais un certain a+h avec h dans ]0;b-a[ :happy3:
par benekire2 » 26 Mar 2010, 14:05
d'accord, je ne connaissais pas cette variante même si elle parait naturelle.
donc comme pour x>a on a -ka :
-2k/(b-a)
c'est ça ? Je suis pas sur.
donc comme pour x>a on a -k
-2k/(b-a)
c'est ça ? Je suis pas sur.
par Nightmare » 26 Mar 2010, 16:45
L'exercice n'est pas facile et demande réflexion donc je te laisse réfléchir dessus. Pour info, c'est un exercice réarrangé d'un oral des mines. Les élèves se sont bien débrouillés dessus aujourd'hui, mais j'ai dû les lancer.
Comme je te l'ai dit, on a avec epsilon une fonction qui tend vers 0, ie, quel que soit e, à partir d'un certain A, |\le e)
.
On se fixe alors un
. L'idée est d'appliquer le TAF à sur les segments 
et 
puis d'utiliser la croissance de f'.
Comme je te l'ai dit, on a
On se fixe alors un
par benekire2 » 26 Mar 2010, 17:08
ba écoute je vais y réfléchir ( dès que j'aurais fini ce que je fais )
Rapidement , je trouve que :
<2)
h entre 0 et e
<2)
h entre 0 et e
C'est ça ou je me suis trompé ?
En fait, je cois a quoi on veut arriver avec la croissance . Mais j'ai pas du tout l'impression que moi je suis partit sur ces bases. Mon truc ne ressemble pas a grand chose. J'ai un peu l'impression d'avancer dans le noir pour cet exercice ...
Rapidement , je trouve que :
h entre 0 et e
h entre 0 et e
C'est ça ou je me suis trompé ?
En fait, je cois a quoi on veut arriver avec la croissance . Mais j'ai pas du tout l'impression que moi je suis partit sur ces bases. Mon truc ne ressemble pas a grand chose. J'ai un peu l'impression d'avancer dans le noir pour cet exercice ...
par benekire2 » 26 Mar 2010, 20:44
est-ce que mes deux encadrements sont justes déjà ? Est-ce la bonne voie ?
par Nightmare » 27 Mar 2010, 14:51
Salut !
Les encadrement sont bons. Avant de continuer, je vais noter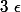
à la place de e et remplacer la fonction 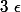par 
.
En appliquant le TAF sur
et 
, on a l'existence de h1 et h2 tels que -\lambda(x)=\epsilon\lambda'(x+h_{1}))
et -\lambda(x-\epsilon)=\epsilon\lambda'(x-h_{2}))
. Ca tu l'as bien trouvé.
Du coup, on a plutot|\le 2)
et |\le 2)
.
Maintenant, la croissance de f' intervient pour comparer f'(x) à f'(x+h1). En l'occurrence, on a par exemple :
\le e^{-x}f'(x+h_{1})=e^{h_{1}}(1+\lambda(x+h_{1})+\lambda'(x+h_{1}))\le e^{\epsilon}(3+\epsilon))
.
On se rend compte que cet encadrement n'est pas assez précis. Il faudrait donc préciser l'encadrement de départ. En l'occurrence, si par exemple au lieu de prendre|\le \epsilon)
à partir d'un certain réel, on prend |\le \epsilon^{2})
.
Du coup, le TAF donne les encadrements|\le 2\epsilon)
et |\le 2\epsilon)
.
On obtient alors :
\le e^{-x}f'(x+h_{1})=e^{h_{1}}(1+\lambda(x+h_{1})+\lambda'(x+h_{1}))\le e^{\epsilon}(1+\epsilon^{2}+2\epsilon)=e^{\epsilon}(1+\epsilon)^{2})
et :
\ge e^{-x}f'(x-h_{2})=e^{-h_{2}}(1+\lambda(x-h_{2})+\lambda'(x-h_{2}))\ge e^{-\epsilon}(1-2\epsilon-\epsilon^{2}))
.
Je te laisse essayer de conclure.
Les encadrement sont bons. Avant de continuer, je vais noter
En appliquant le TAF sur
Du coup, on a plutot
Maintenant, la croissance de f' intervient pour comparer f'(x) à f'(x+h1). En l'occurrence, on a par exemple :
On se rend compte que cet encadrement n'est pas assez précis. Il faudrait donc préciser l'encadrement de départ. En l'occurrence, si par exemple au lieu de prendre
Du coup, le TAF donne les encadrements
On obtient alors :
et :
Je te laisse essayer de conclure.
par benekire2 » 27 Mar 2010, 15:14
alors si je réécrit on a :
^2\le e^{-x}f'(x) \le e^{\epsilon}(1-\epsilon)^2)
Je mettrais bien qu'a epsilon petit, grace a l'approximation affine on a
et de même 
Après ça doit être de la manipulation epsilonesque même si je vois que "ça tend" vers 1 ...
Je mettrais bien qu'a epsilon petit, grace a l'approximation affine on a
Après ça doit être de la manipulation epsilonesque même si je vois que "ça tend" vers 1 ...
par Nightmare » 27 Mar 2010, 15:21
Attention, à gauche on avait 1-e²-2e qui n'est pas égal à (1-e)² 
Tout ce qu'il faut pour conclure, c'est qu'on peut toujours avoir un encadrement du type < e^{\epsilon}(1+\epsilon)^{2} < 1+\alpha)
Tout ce qu'il faut pour conclure, c'est qu'on peut toujours avoir un encadrement du type
par benekire2 » 27 Mar 2010, 15:36
a ba oui ... j'avais mal lu ton truc ..
Alors en développant avec e^-epsilon=1-epsilon et e^epsilon=1+epsilon j'arrive au résultat :
<1-(3\epsilon-\epsilon^2-\epsilon^3)<e^{-x}f'(x)<1+(3\epsilon+3\epsilon^2+\epsilon^3))
Alors en développant avec e^-epsilon=1-epsilon et e^epsilon=1+epsilon j'arrive au résultat :
par Nightmare » 27 Mar 2010, 15:54
Il n'y a pas besoin de développer !
Pour tout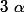
, il existe un (dans 
) tel que  < e^{\epsilon}(1+\epsilon)^{2} < 1+\alpha)
.
D'après les inégalité qu'a fournit le TAF, à cet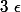 est associé un réel A tel que dès que 
on ait \le 1+\alpha)
.
Ceci prouve que exp(-x)f'(x) converge vers 1 en +oo.
L'exercice en lui-même n'est pas difficile car c'est une méthode "classique", mais c'est un très bon entrainement je pense pour justement manier ces démonstrations un peu formelles et lourdes.
Pour tout
D'après les inégalité qu'a fournit le TAF, à cet
Ceci prouve que exp(-x)f'(x) converge vers 1 en +oo.
L'exercice en lui-même n'est pas difficile car c'est une méthode "classique", mais c'est un très bon entrainement je pense pour justement manier ces démonstrations un peu formelles et lourdes.
par benekire2 » 27 Mar 2010, 16:17
oui c'est très bien comme exercices. C'est des choses nouvelles par rapport à ce que j'ai l'habitude de faire.
par benekire2 » 27 Mar 2010, 16:28
j'ai un peu la flemme de faire la I-b mais j'ai quand même un peu envie ^^
Tu dis que l'on admet que seules les homothéties sont des applications linéaires continues de R dans R.
Mais pour moi une homotétie c'est de R² dans R² ... ou alors nous n'avons pas la même définition de l'homotétie.
Tu dis que l'on admet que seules les homothéties sont des applications linéaires continues de R dans R.
Mais pour moi une homotétie c'est de R² dans R² ... ou alors nous n'avons pas la même définition de l'homotétie.
80 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :