Khôlle : Exponentielle et équadiff

[Nightmare]

Salut :happy3:

Voici les trois exercices de la semaine prochaines, par ordre de difficulté.

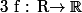
I] Trouver les applications vérifiant l'équation fonctionnelle si :
.a) f est dérivable
.b) f est seulement supposée continue.


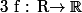
II] Soit continue et ayant une limite finie en .

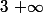
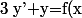Montrer que toutes les solutions de l'équation différentielle ont aussi une limite finie en


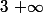
III] Soit dérivable et de dérivée croissante.

On suppose que . Montrer que .

Indications :

I]b) On pourra admettre ou démontrer que les seules applications linéaires et continues de R dans R sont les homothéties

II] Il est possible d'exprimer les solutions de l'équation différentielle en fonction de f

III] On admettra le théorème suivant : Etant donné deux points A=(a,f(a)) et B=(b,f(b)) sur le graphe d'une fonction f dérivable. Il existe un point C=(c,f(c)), a <= c <= b tel que la tangente au graphe en C soit parallèle à (AB). (Nom du théorème ?)

Bon courage
:happy3:

[benekire2]

c'est le théorème des accroissements finis ...
Je regarderais cela quand j'aurais un peu de temps !!

[benekire2]

Pour le I a:
Supposons qu'il existe a tel que f(a)=0 , on aurait f(a)f(x)=0 ie f est identiquement nulle. Supposons ce cas exclu. f ne s'annule pas .
On a :
f(x)=f²(x/2)>0

maintenant, avec y=0 f(x)=f(x)f(0) ie f(0)=1

Maintenant à y fixé f'(x+y)=f(y)f'(x) ie y'=ay avec f(0)=1 ie f(x)=e^(ax)

la réciproque est évidente. Un peu flouté pour le b :doh:

[benekire2]

Pour le II :

On montre facilement qu'avec p(x) une solution particulière de l'équation différentielle toutes les solutions sont :

C.e^(-x)+p(x) comment les exprimer en fonction de f(x) ??

[Nightmare]

Salut :happy3:

Alors :

Supposons qu'il existe a tel que f(a)=0 , on aurait f(a)f(x)=0 ie f est identiquement nulle.

Pourquoi f identiquement nulle?

Maintenant à y fixé f'(x+y)=f(y)f'(x) ie y'=ay avec f(0)=1 ie f(x)=e^(ax)

Quelques problèmes de rédaction. Pourquoi introduire une autre lettre y ? Qui plus est elle est déjà utilisée en tant que variable.

Ici, on pose x=0, on obtient pour tout y, f'(y)=f'(0)f(y). D'où effectivement

Bref, c'était la partie facile :lol3:

Pour le II] je t'y laisse y réfléchir un peu plus longtemps :happy3:

[benekire2]

f identiquement nulle, je veut dire nulle.
pour le y j'ai précisé qu'il était fixé. Mais comme tu l'as dit c'était la partie facile...

Pour la II .. je vais chercher, mais je promet rien !

[Nightmare]

Oui mais je n'ai pas compris ta justification du fait que si f s'annule une fois alors elle est identiquement nulle.

[benekire2]

Je peut ramener à C.e^-x +f(x)-p'(x) ... mais bon ça n'avance probablement pas a grand chose.

[benekire2]

A ba oui pour la justification, en effet c'est pas bon, supposons a tel que f(a)=0
alors f(a+x)=0 et donc nécessairement f(x)=0

[Nightmare]

Pour la II] on pourra multiplier l'équation par exp(x).

[alavacommejetepousse]

Pour le II :

On montre facilement qu'avec p(x) une solution particulière de l'équation différentielle toutes les solutions sont :

C.e^(-x)+p(x) comment les exprimer en fonction de f(x) ??

bonsoir puisque tu sembles vouloir " t avancer" regarde donc qq la méthode (générale) de la " variation de la constante même si ici ce n est pas necessaire

[benekire2]

Je vais pas pouvoir y réfléchir aujourd'hui et peut être pas demain non plus. J' ai ( encore ... ) une grosse fièvre . Mercredi c'est JAPD .. alors je promet de m'y mettre jeudi !!

[benekire2]

mais bon, hier j'étais arriver a : grâce à ton astuce , avec k une constante.

Je pense que je m'approche.

[Nightmare]

Salut,

Modulo la variable d'intégration et les bornes, c'est bien ça !

[benekire2]

euh c'est a dire, pour les bornes, c'est une primitive, donc au pire je met de x0 à x mais pour la variable d'intégration j'ai une question :

e^x est en fonction de x mais f est en fonction de x ?

EDIT:

En fait, j'ai fais une erreur, c'est :

[Nightmare]

J'ai pas vraiment compris ta question sur la variable. Une variable est muette donc peut importe la lettre qu'on utilise, ce qu'il faut par contre c'est distinguer la variable de la fonction y et la variable d'intégration, ce que tu as bien fait à la fin. (au passage, on peut supposer , pourquoi?)

[benekire2]

Oui mais je me suis rendu compte de la connerie que j'ai écrite alors j'ai édité !

On peut supposer x0=0 parce que il suffit de rajouter une constante pour avoir les autres primitives.

[Nightmare]

C'est bien ça. Reste à terminer !

[benekire2]

J'ai essayé de l'intégrer par partie, ça donne pas grand chose.

[benekire2]

sinon j'ai pensé a autre chose. Pour tout e positif; il existe A tels que t>A => |f(t)-l|donc en utilisant la définition de la limite on devrait arriver a encadrer l'intégrale. Mais on je vais y réfléchir.