606 résultats trouvés
Revenir à la recherche avancée
Re: Fabrique à nombre premiers....
Oui bien sûr, c'est vrai que c'est pas clair en relisant ce que j'ai écrit.
- 20 Déc 2018, 23:53
- Forum: ⚔ Défis et énigmes
- Sujet: Fabrique à nombre premiers....
- Réponses: 6
- Vues: 1083
Re: Fabrique à nombre premiers....
Si je ne m'abuse, si tous les ap + bq sont premiers pour p,q premiers >= N alors les a(ap + bq) + b(aq +bp) le sont aussi (car ap + bq et aq + bp sont premiers >= N). Dés lors les (a²+b²)p + (2ab)q sont premiers pour p,q premiers >=N Si on construit alors (a(n+1), b(n+1) ) = (a(n)² + b(n)² , 2a(n)b(...
- 18 Déc 2018, 04:13
- Forum: ⚔ Défis et énigmes
- Sujet: Fabrique à nombre premiers....
- Réponses: 6
- Vues: 1083
Re: Trés convexe
Quitte à poser g(x) = f(x) - f(0) , on peut supposer que f(0)=0 . Pour y=-x on obtient f(x)+f(-x) \geq 4|x| On montre ensuite par récurrence que f(2^nx) \geq 2^{n+1} n |x| + 2^nf(x) En sommant avec l'inégalité obtenue en -x , on a : f&#...
- 27 Mar 2018, 04:08
- Forum: ⚔ Défis et énigmes
- Sujet: Trés convexe
- Réponses: 2
- Vues: 700
Re: Formes quadratiques
H et G sont des sev de R^n donc dim(H+G) <= ?
De plus dim(H+G) = ?
De plus dim(H+G) = ?
- 10 Nov 2017, 03:45
- Forum: ✯✎ Supérieur
- Sujet: Formes quadratiques
- Réponses: 25
- Vues: 1325
Re: Combinatoire élémentaire
D'après le lemme des tiroirs il y a un des 6 ensembles qui contient au moins 337 éléments. Sans perte de généralités, supposons que c'est f-1({1}). On ordonne cet ensemble selon (a_i) croissante et on regarde les (au moins) 336 éléments (a_i-a_1). S'ils sont dans f-1({1}) alors on a terminé. Sinon c...
- 03 Nov 2017, 08:04
- Forum: ⚔ Défis et énigmes
- Sujet: Combinatoire élémentaire
- Réponses: 2
- Vues: 771
Re: Séquence de nombres
An other way to do it would be to show by induction that for i \in [|2;k|] , a_1a_j \equiv a_1 (n) (using the fact that a_{i-1}a_i \equiv a_i (n) ). Therefore a_1a_k \equiv a_1 (n) , so a_k(a_1-1) \equiv a_1-a_k (n) . Since a_1 and a_k are different and \leq n...
- 19 Oct 2017, 21:56
- Forum: ⚔ Défis et énigmes
- Sujet: Séquence de nombres
- Réponses: 6
- Vues: 875
Re: Fraction "successives".
Si il y en a qui veulent chercher, en fait la partie assez facile, c'est dans le sens "si bc-ad=1 alors a/b et c/d sont successives" Bizarrement, dans l'autre sens : "si bc-ad>=2 alors a/b et c/d ne sont pas successives" , c'est nettement moins évident (*) alors que normalement,...
- 16 Oct 2017, 12:11
- Forum: ⚔ Défis et énigmes
- Sujet: Fraction "successives".
- Réponses: 48
- Vues: 2749
Re: logique ensembles algebre
Tu peux montrer par récurrence que ca vaut (x+1)...(x+n)/n!
- 17 Sep 2017, 21:08
- Forum: ✯✎ Supérieur
- Sujet: logique ensembles algebre
- Réponses: 5
- Vues: 691
Re: approximation d'un irrationnel
Vu que racine de 2 est irrationnelle, l'ensemble des \{n\sqrt2\} (partie fractionnaire) est dense dans [0,1]. En particulier pour tout \alpha de [0,1] il existe une suite a_n d'entiers telle que \{a_n\sqrt2\} converge vers \alpha . Alors, E(a_n\sqrt2) = -\{a_n\sqrt2\} + a_n\sqrt2\ = -\alpha ...
- 06 Juil 2017, 02:32
- Forum: ⚔ Défis et énigmes
- Sujet: approximation d'un irrationnel
- Réponses: 2
- Vues: 922
Re: Facile et simple ne sont pas confondus
Sauf erreur,
si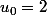 alors
alors 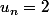
et si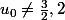 alors
alors 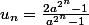 avec
avec 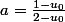
si
et si
- 05 Juil 2017, 21:23
- Forum: ⚔ Défis et énigmes
- Sujet: Facile et simple ne sont pas confondus
- Réponses: 197
- Vues: 8503
Re: Classe d'un entier dans Z/bZ
Ecris de deux manières différentes le produit des f(x) pour x dans (Z/bZ)* J'ai ça : \prod_{a \in (Z/bZ)*} f(\bar a) = \prod_{a \in (Z/bZ)*} \bar {10} \bar a Ensuite je vois pas trop quoi faire L'ensemble des f(x) c'est quoi ? Donc faire le produit des f(x) ca revient à fair...
- 05 Juil 2017, 13:16
- Forum: ✯✎ Supérieur
- Sujet: Classe d'un entier dans Z/bZ
- Réponses: 21
- Vues: 1083
Re: Classe d'un entier dans Z/bZ
Ecris de deux manières différentes le produit des f(x) pour x dans (Z/bZ)*
- 04 Juil 2017, 18:26
- Forum: ✯✎ Supérieur
- Sujet: Classe d'un entier dans Z/bZ
- Réponses: 21
- Vues: 1083
Re: Classe d'un entier dans Z/bZ
C'est quoi pour toi 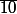 ?
?
- 04 Juil 2017, 13:20
- Forum: ✯✎ Supérieur
- Sujet: Classe d'un entier dans Z/bZ
- Réponses: 21
- Vues: 1083
Re: application lipschitzienne
Quel est le M optimal que tu pourrais prendre ?
- 03 Juil 2017, 23:46
- Forum: ✯✎ Supérieur
- Sujet: application lipschitzienne
- Réponses: 10
- Vues: 1044
Re: Suite dérivée de la suite de Fibonacci
Il suffit de prendre l'écriture de type F_n = \frac{1}{\sqrt5} (\alpha^n-\beta^n) et de développer l'expression F_nF_{n+2}-F_{n+1}^2 en fonction de \alpha et \beta . Cela se simplifie correctement et il suffit de factoriser par (\alpha \beta)^n . Une autre méthode serait de voir F_nF...
- 01 Juil 2017, 19:17
- Forum: ✯✎ Supérieur
- Sujet: Suite dérivée de la suite de Fibonacci
- Réponses: 6
- Vues: 1349
Re: Nilpotence matrice triangulaire supèrieur diagonale null
infernaleur a écrit:Salut !
Je m’intéressais à démontrer la nilpotence d'une matrice triangulaire supérieur à diagonale nulle mais je n'y parviens pas ...
Auriez-vous quelques pistes à me donner
Merci !!!
Que vaut son polynôme caractéristique ?
- 27 Juin 2017, 23:35
- Forum: ✯✎ Supérieur
- Sujet: Nilpotence matrice triangulaire supèrieur diagonale nulle
- Réponses: 6
- Vues: 7164
Re: Facile et simple ne sont pas confondus
pour la 21 soit n un entier , la la fonction qu'on cherche à majorée sur [n-1;n+2] f est bornée car continue sur un compact donc majorée par Mn. Soit Fn définie par : Fo = Mo sur [0;1] F1= fonction linéaire qui vaut M1 en 1 et M2 en 2 Fn+1 définie sur [n;n+1] : _ vaut Mn si Mn+1<= Mn _ est une fonc...
- 27 Juin 2017, 02:39
- Forum: ⚔ Défis et énigmes
- Sujet: Facile et simple ne sont pas confondus
- Réponses: 197
- Vues: 8503
Re: Facile et simple ne sont pas confondus
Faut que tu places des quantificateurs parce que là c'est pas clair.
Bien sûr à m fixé il existe N tq 1/|sin(m)| < 2N/m (car 2N/m tend vers + inf quand N tend vers +inf)
Mais si quelque soit m<N , 1/|sin(m)| < 2N/m alors comme je l'ai écrit auparavant, la suite (1/|sin(n)|) est bornée.
Bien sûr à m fixé il existe N tq 1/|sin(m)| < 2N/m (car 2N/m tend vers + inf quand N tend vers +inf)
Mais si quelque soit m<N , 1/|sin(m)| < 2N/m alors comme je l'ai écrit auparavant, la suite (1/|sin(n)|) est bornée.
- 21 Juin 2017, 18:02
- Forum: ⚔ Défis et énigmes
- Sujet: Facile et simple ne sont pas confondus
- Réponses: 197
- Vues: 8503
Re: Facile et simple ne sont pas confondus
Je ne comprends pas sa justification pour la majoration de 1/|sin(m)|.
Car en prenant m=N-1 on obtient 1/|sin(N-1)| < 2N/(N-1) < 3 à partir d'un certain rang, et cela suggère que 1/|sin(i)| est bornée (ce qui est faux).
Car en prenant m=N-1 on obtient 1/|sin(N-1)| < 2N/(N-1) < 3 à partir d'un certain rang, et cela suggère que 1/|sin(i)| est bornée (ce qui est faux).
- 21 Juin 2017, 16:36
- Forum: ⚔ Défis et énigmes
- Sujet: Facile et simple ne sont pas confondus
- Réponses: 197
- Vues: 8503
Re: somme des n premier entier à la puisance p
Oui bien sûr, encore faut il que tu nous envoies ce que tu as fait.
- 19 Juin 2017, 00:47
- Forum: ✯✎ Supérieur
- Sujet: somme des n premier entier à la puisance p
- Réponses: 25
- Vues: 1735
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
