Montrer que
Séquence de nombres
7 messages
- Page 1 sur 1
Séquence de nombres
Soit  un entier strictement positif et soit
un entier strictement positif et soit 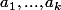 , avec
, avec 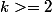 , des entiers strictement positifs distincts appartenant `a l’ensemble
, des entiers strictement positifs distincts appartenant `a l’ensemble 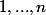 tels que n divise
tels que n divise ) pour
pour
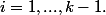
Montrer que ne divise pas
ne divise pas ) .
.
Montrer que
Re: Séquence de nombres
Salut,
Pour tout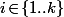 posons
posons 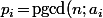) et
et 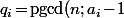) .
.
(1) et
et 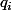 sont premiers entre eux (car
sont premiers entre eux (car 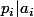 et
et 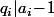 ) et divisent tout les deux
) et divisent tout les deux  donc
donc 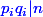 .
.
(2) Pour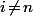 l'hypothèse
l'hypothèse ) nous dit que,
nous dit que, ) .
.
Or\!=\!1) donc
donc  c'est à dire
c'est à dire ) ou encore
ou encore 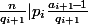 .
.
Mais\!=\!1) donc en fait
donc en fait 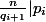 c'est à dire
c'est à dire 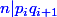 .
.
(3) De (1) et (2) on déduit que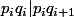 c'est à dire que
c'est à dire que 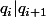 et, si
et, si 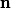 divisait
divisait ) , on aurait aussi
, on aurait aussi 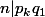 (idem (2)) donc
(idem (2)) donc 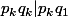 c'est à dire
c'est à dire 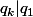 et tout les
et tout les 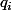 seraient égaux (à un certain
seraient égaux (à un certain  ).
).
Or dans ce cas, le (1) nous dirait que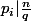 et le (2) que
et le (2) que 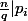 donc les
donc les  seraient aussi tous égaux à un certain
seraient aussi tous égaux à un certain  avec
avec 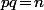 et
et \!=\!1)
Mézalors, pour tout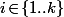 on aurait
on aurait 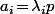 avec
avec 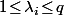 (car
(car 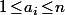 ) et, comme
) et, comme 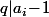 on aurait
on aurait 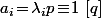 or, comme
or, comme \!=\!1) , il y a une unique solution
, il y a une unique solution 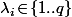 à cette congruence donc en fait tout les
à cette congruence donc en fait tout les  sont égaux.
sont égaux.
P.S. Donc on peut même "diminuer" l'hypothèse de départ en supposant uniquement que les ne sont pas tous égaux plutôt que de les supposer (deux à eux) distincts.
ne sont pas tous égaux plutôt que de les supposer (deux à eux) distincts.
Pour tout
(1)
(2) Pour
Or
Mais
(3) De (1) et (2) on déduit que
Or dans ce cas, le (1) nous dirait que
Mézalors, pour tout
P.S. Donc on peut même "diminuer" l'hypothèse de départ en supposant uniquement que les
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Séquence de nombres
Thanks Ben314, but I don't understand... 
Someone can traslate it in english??
Thanks

Someone can traslate it in english??
Thanks
Re: Séquence de nombres
For 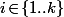 let
let ) and
and ) .
.
(1) and
and 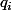 are coprimes (because
are coprimes (because 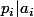 and
and 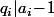 ) and both of them divides
) and both of them divides  so
so 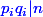 .
.
(2) For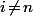 we know that
we know that ) so
so ) .
.
But\!=\!1) so, in fact,
so, in fact,  so
so ) and
and 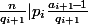 .
.
But\!=\!1) sot
sot 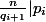 and
and 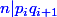 .
.
(3) From (1) and (2) we deduct that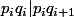 so
so 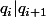 .
.
If we supose further that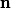 divides
divides ) , we have
, we have 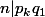 (same as (2)) so
(same as (2)) so 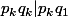 and
and 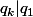 witch mean that all the
witch mean that all the 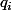 are same (equal to some integer
are same (equal to some integer  ).
).
But, in this case (1) say that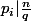 and (2) say that
and (2) say that 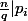 so the
so the  ares same and are equal to some integer
ares same and are equal to some integer  with
with 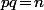 and
and \!=\!1)
Now, for all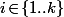 we have
we have 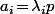 with
with 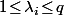 (because
(because 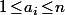 ).
).
We have also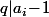 so
so 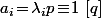 but this équation have only one solution
but this équation have only one solution 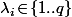 (because
(because \!=\!1) ) so all the
) so all the  are same.
are same.
(1)
(2) For
But
But
(3) From (1) and (2) we deduct that
If we supose further that
But, in this case (1) say that
Now, for all
We have also
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Séquence de nombres
Il faudrait que n divise le plus grand nombre de la suite A et aussi A-1, c'est à dire qu'il faudrait que n divise A(A-1), n serait alors plus grand que les autres produits.
Si j'ai bien compris l'énoncé.
Si j'ai bien compris l'énoncé.
Re: Séquence de nombres
An other way to do it would be to show by induction that for 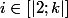 ,
, ) (using the fact that
(using the fact that ) ).
).
Therefore) , so
, so  \equiv a_1-a_k (n)) . Since
. Since  and
and  are different and
are different and 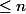 , we can't have
, we can't have ) . Then it follows that
. Then it follows that  doesn't divide
doesn't divide ) .
.
Therefore
Re: Séquence de nombres
Thanks Ben314, 
I understand all exept the final part.
Can you explain better the final part? (where is exactly the absurd and why there is only one solution?)
And what mean in english "
Donc on peut même "diminuer" l'hypothèse de départ en supposant uniquement que les ne sont pas tous égaux plutôt que de les supposer (deux à eux) distincts." ?
ne sont pas tous égaux plutôt que de les supposer (deux à eux) distincts." ?
I understand all exept the final part.
Can you explain better the final part? (where is exactly the absurd and why there is only one solution?)
And what mean in english "
Donc on peut même "diminuer" l'hypothèse de départ en supposant uniquement que les
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
