Classe d'un entier dans Z/bZ

[mehdi-128]

Bonjour,

Soit b un nombre premier supérieur ou égal à 2 distinct de 2 et de 5. b est premier avec 10.
On note la classe d'un entier a dans

1/ Démontrer que l'application :

est bien définie et injective.

Déjà comment savoir que appartient à ?
Si b=3 par exemple :
Alors là je bloque puisque 10 barre n'y est pas ...

Pour l'injectivité je pense à calculer le noyau de f...

2/ En utilisant la question précédente, montrer que

Merci.

[zygomatique]

salut

visiblement tu ne connais rien des congruences ...

par définition (pour tout b)

et puisque b est un premier différent de 2 et de 5 donc forcément différent de 10 !!! parce qu'il est premier
et forcément premier avec 10 puisque p n'est ni 2 ni 5 alors

puisque le théorème de Bachet- Bezout dit que ...

[mehdi-128]

salut

visiblement tu ne connais rien des congruences ...

par définition (pour tout b)

et puisque b est un premier différent de 2 et de 5 donc forcément différent de 10 !!! parce qu'il est premier
et forcément premier avec 10 puisque p n'est ni 2 ni 5 alors

puisque le théorème de Bachet- Bezout dit que ...

J'arrive toujours pas à comprendre pourquoi : (pour tout b) y a pas une démo ?

Après si b est premier différent de 2 et 5 et 10=2*5 forcément b est premier avec 10 non ?
Puis ça change quoi si b n'est pas premier avec 10 pour montrer que ?

D'après le théorème de Bezout, si b et 10 sont premiers entre eux il existe u et v entiers relatifs tel que :

ça avance à quoi ?

[mehdi-128]

Avec le théorème de Bezout j'ai réussi à montrer que :

premier avec b équivalent à est inversible dans (Z/bZ)*

[Matt_01]

C'est quoi pour toi ?

[mehdi-128]

C'est quoi pour toi ?

Le reste de la division euclidienne de 10 par b. Ah je viens de comprendre pourquoi il faut b premier avec 10, on veut que ce reste soit non nul car on est dans (Z/bZ)* et pas dans (Z/bZ) !

[zygomatique]

non ...

[Pseuda]

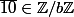
J'arrive toujours pas à comprendre pourquoi : (pour tout b) y a pas une démo ?

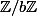
Car les classes d'équivalence de forment une partition de (il y a un recouvrement total de Z par les classes d'équivalence Z/bZ quelque soit b).
Par exemple, si
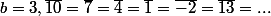
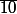
Le reste de la division euclidienne de 10 par b n'est qu'un élément parmi les autres éléments de , le seul compris entre 0 et b-1 (si b=3, c'est 1).

Après si b est premier différent de 2 et 5 et 10=2*5 forcément b est premier avec 10 non ?

Oui. De toute façon, b est un nombre premier différent de 2 et de 5, donc il est premier avec 10 car les seuls nombres premiers qui divisent 10 sont 2 et 5 dont b est différent.

Puis ça change quoi si b n'est pas premier avec 10 pour montrer que ?

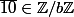
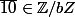
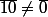
Tu as répondu plus haut. dans tous les cas, mais aussi car si b est premier avec 10 (mais surtout parce que b ne divise pas 10).

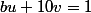
D'après le théorème de Bezout, si b et 10 sont premiers entre eux il existe u et v entiers relatifs tel que : ça avance à quoi ?

Pour répondre à quelle question ?

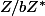
Pour l'injectivité, à mon avis le noyau de f ne va pas marcher, car est un groupe multiplicatif, et f n'est pas un morphisme de ce groupe. Il faut à mon avis revenir à la définition.

[mehdi-128]

Merci pour la définition j'ai fait :

((Z/bZ)* , x ) est un groupe et comme 10 barre est différent de 0 barre on a : appartient bien à (Z/bZ)* donc f est bien définie.

Pour l'injectivité :

Soient et deux éléments de (Z/bZ)*. Supposons : donc :



Or 10 et b sont premiers entre eux car b différent de 2 et 5... Donc 10 barre est un élément inversible de (Z/bZ)* donc il existe c barre tel que :

D'où :

Enfin : donc f est injective.

Après la question 2 je vois pas du tout.

[Matt_01]

Ecris de deux manières différentes le produit des f(x) pour x dans (Z/bZ)*

[zygomatique]

par définition pour tout b quelconque désigne la classe de 10 modulo b donc l'ensemble des entiers 10 + kb avec k entier relatif ...

l'application avec b nombre premier différent de 2 et 5 est évidemment bien définie et injective

et (Z/bZ)* est un groupe multiplicatif ...

puisque b est premier il est évidemment premier avec 10 donc il existe u et v tels que

et évidemment (je ne mets plus les barres)

10a = 10c <=>10(a - c) = 0 <=> u10(a - c) = 0 <=> a - c = 0 <=> a = c

[zygomatique]

puisque (Z/bZ)* est un groupe multiplicatif de cardinal b - 1 il est évident que 10^(b - 1) = 1 (théorie des groupes)

de façon plus élémentaire : 10^1, 10^2, ..., 10^(b - 1) sont b - 1 éléments de (Z/bZ)*

puisque l'application f : a --> 10a est injective on l'applique à ces puissances de 10 et on considère les deux cas :

toutes les puissances de 10 sont distinctes (modulo b)
il en existe (au moins) 2 congrues (modulo b

... enfin faut voir ...

[mehdi-128]

Ecris de deux manières différentes le produit des f(x) pour x dans (Z/bZ)*

J'ai ça :

Ensuite je vois pas trop quoi faire

[mehdi-128]

puisque (Z/bZ)* est un groupe multiplicatif de cardinal b - 1 il est évident que 10^(b - 1) = 1 (théorie des groupes)

de façon plus élémentaire : 10^1, 10^2, ..., 10^(b - 1) sont b - 1 éléments de (Z/bZ)*

puisque l'application f : a --> 10a est injective on l'applique à ces puissances de 10 et on considère les deux cas :

toutes les puissances de 10 sont distinctes (modulo b)
il en existe (au moins) 2 congrues (modulo b

... enfin faut voir ...

Vous utilisez le théorème de Lagrange: ?

[Matt_01]

Ecris de deux manières différentes le produit des f(x) pour x dans (Z/bZ)*

J'ai ça :

Ensuite je vois pas trop quoi faire

L'ensemble des f(x) c'est quoi ? Donc faire le produit des f(x) ca revient à faire quel produit ?

[mehdi-128]

Ecris de deux manières différentes le produit des f(x) pour x dans (Z/bZ)*

J'ai ça :

Ensuite je vois pas trop quoi faire

L'ensemble des f(x) c'est quoi ? Donc faire le produit des f(x) ca revient à faire quel produit ?

f est injective et card(ensemble de départ)=card(ensemble d'arrivée) donc f est une bijection de (Z/bZ)* dans (Z/bZ)* ... Faire le produit des f(x) revient à faire le produit des x :



Donc :

J'ai bien le droit de sortir de 10 barre du produit vu qu'il dépend pas de a ?

[zygomatique]

c'est faux



et la conclusion est immédiate ...

[mehdi-128]

c'est faux



et la conclusion est immédiate ...

Bien vu !

Je poursuis :



Or, b est un nombre premier donc que dire de 1,2,...,b-1 ?

Si j'arrive à prouver qu'ils sont premiers avec b je peux utiliser le fait que tous ces nombres seraient inversibles dans (Z/bZ)* et simplifier.

[zygomatique]

mais tu as et

un peu de sérieux !!! qu'en déduit-on immédiatement ?

[mehdi-128]

mais tu as et

un peu de sérieux !!! qu'en déduit-on immédiatement ?

Comment savez vous que : ?