Trés convexe
3 messages
- Page 1 sur 1
Re: Trés convexe
par Matt_01 » 27 Mar 2018, 04:08
Quitte à poser  = f(x) - f(0))
, on peut supposer que =0)
.
Pour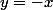
on obtient +f(-x) \geq 4|x|)
On montre ensuite par récurrence que \geq 2^{n+1} n |x| + 2^nf(x))
En sommant avec l'inégalité obtenue en
, on a :
+f(-2^nx) \geq 2^{n+2}n |x| + 2^n(f(x)+f(-x)) \geq 2^{n+2}(n+1)|x|)
En évaluant en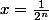
on obtient :
+f(-1) \geq 4(n+1))
et donc il n'existe pas de telle fonction.
Pour
On montre ensuite par récurrence que
En sommant avec l'inégalité obtenue en
En évaluant en
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :