Application lipschitzienne

[pierresimpore]

Bonsoir,
On considere l'espace muni de la norme et l'application
telle que .

a) Montrer que est lipschitzienne sur . est-elle lineaire?

b) soit la suite de telle que . montrer qu'elle converge dans . determiner .
mes elements de reponses:
a) j'ai appliqué la definition: soit u et v element de E alors



On sait que et aussi de plus

donc . Voilà je bloque à partir de là. comment faire sortir ?

[Arbre]

Bonsoir,

Pour posséde un majorant en rapport avec la nome sup, non ?

[pierresimpore]

Bonsoir, je comprends pas bien, comme u et v sont des applications continues, donc elles sont bornées. on peut donc dire qu'il existe un M tel que
, en integrant de chaque coté, je n'obtiens pas ce que je veux.

[Matt_01]

Quel est le M optimal que tu pourrais prendre ?

[pierresimpore]

Bonsoir, desolé mais je ne connais pas

[aviateur]

Bonjour
Il faut bien comprendre de quoi est muni (i.e de quelle norme) ton espace vectoriel E:
pour par def.

Donc dans ton intégrale la majoration "naturelle" est: pour tout :

[pierresimpore]

je savais pas que , ca resoud la premiere question: donc on aura
par consequent est lipschitzienne.

[pierresimpore]

maintenant pour la convergence de , j'ai juste calculé la limite et je trouve
qui est element de

[aviateur]

Bonjour, Je n 'ai pas fait les calculs mais disons que ponctuellement
(i.e limite simple) U_n cv vers U: t -> . Donc on peut conjecturer ta réponse.
Cependant tu dis "avoir calculé la limite". Est ce que cela signifie que tu as montré que cv vers U au sens de la norme dans E?

[pierresimpore]

Bonjour, j'ai juste fait le calcul. Apparemment je ne maitrise pas trop la notion d'espace vectoriel normé.



donc

ce qui donne qui est dans E.
c'est ce que j'ai fai

[aviateur]

Bonjour Là tu dois faire un effort de compréhension.
Mais je peux te faire une synthèse:
En gros tu retiens que si ton E-v est de dimension finie tout les normes sont équivalentes et dans ce cas la notion de limite ne dépend pas de la norme.

Par contre si l'e-v est de dimension infinie la notion de limite dépend de la norme.
Donc tu peux avoir une suite (u_n) (dans un espace E) qui converge vers un élément de E que j'appelle
L (pour une certaine norme) qui converge ailleurs (ou ne converge pas pour une autre norme).

Je t'invite à comprendre cela, on doit pouvoir trouver des exemples un peu partout.

De façon générale si tu as un e-v normé (E,N) (N est la norme) on dit que U_n converge vers E (au sens de la norme N) si et seulement si tend vers 0.

C'est important à savoir cela. D'abord c'est la définition et puis c'est pratique puisqu'on est toujours ramené à montrer que une suite de positif (ici ) converge vers 0.

On revient donc à ton exercice. Je désigne par L l'élément de E qui est la fonction défnie par

Il est clair que que pour chaque t, . Il s'agit d'une limite ponctuelle. On dit que L est la limite "simple" de la suite U_n. Mais cela ne montre pas que U_n converge vers L au sens de la norme de E.
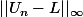
Ceci étant dit on peut espérer que U_n cv vers L au sens de la norme de E. Mais si tu as compris mes explications tu dois montrer que tend vers 0.