Fabrique à nombre premiers....

[Ben314]

Salut,

Peut-on trouver trois entiers naturels non nuls 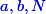tels que, quelque soient les nombres premiers distincts , le nombre soit lui aussi premier ?

P.S. : Il n'est pas utile d'utiliser de "gros outils" style répartition des nombres premiers ou théorème de Dirichlet donc on peut le faire avec un niveau "Lycée". (mais c'est pas mal astucieux...)

[aviateur]

Bonjour
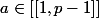
La réponse est non puisque pour tout nombre premier p et tout il existe une infinité de nombre premier P congru à a modulo p.
Mais s'il faut se restreindre à des connaissances de Terminale??

[Ben314]

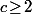
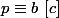
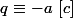
Effectivement, en utilisant le Théorème de Dirichlet (j'espère ne pas me gourer sur le nom du théorème que tu utilise), c'est facile : une fois a et b fixés, tu prend un nombre premier à la fois avec et avec : il existe une infinité de premier tels que et une infinité de premier tels que et pour de tout tel couple on a qui divise .

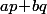
Mais il y a aussi une preuve niveau Lycée (en ce qui concerne les théorèmes/résultats utilisés).

[descampsh]

Que vous êtes tous vraiment doués en mathématique, je suis un peu faible dans ce matière, c'est pour cela que j'ai consulté souvent ce forum pour avoir des réponses et des bonnes explications sur un tel sujet. Merci à vous de nous avoir aidé.

[Matt_01]

Si je ne m'abuse, si tous les ap + bq sont premiers pour p,q premiers >= N alors les a(ap + bq) + b(aq +bp) le sont aussi (car ap + bq et aq + bp sont premiers >= N).
Dés lors les (a²+b²)p + (2ab)q sont premiers pour p,q premiers >=N
Si on construit alors (a(n+1), b(n+1) ) = (a(n)² + b(n)² , 2a(n)b(n) ), on voit que b(n+1) est divisible par tous les éléments de Pn = { p premier tq p divise a(i) pour i<=n}
Si l'union des Pn est finie alors b(n) et a(n) ne seront pas premiers entre eux à partir d'un certain rang => les a(n)p + b(n)q ne peuvent pas être tous premiers.
Si l'union des Pn est infinie on pourra trouver p' et q' premiers distincts >= N tels que p' divise a(i) et q' divise a(j) avec i < j.
Mais alors b(j) est divisible par p' et donc a(j)p' + b(j)q' est divisible par p'q' et donc non premier.

L'idée c'est en fait de voir que l'énoncé est facile à montrer lorsqu'on peut prendre pour p et q certains diviseurs de a et b, et d'alors se ramener via la transformation (a,b) -> (a²+b², 2ab) à des couples d'entiers avec des diviseurs premiers suffisament grands (et qui contournent ainsi la contrainte p,q >= N).

[Ben314]

Oui, c'est bien ça.
En précisant bien (vu que c'est pas clair vu la façon dont tu l'écrit) que
Pn = { p premier tq p divise au moins un a(i) pour i<=n}
(i.e. c'est un "il existe i<=n tel que" et pas un "pour tout i<=n")

[Matt_01]

Oui bien sûr, c'est vrai que c'est pas clair en relisant ce que j'ai écrit.