585 résultats trouvés
Revenir à la recherche avancée
Re: Suites et équivalents
L'énoncé indique que c'est le même raisonnement. Tu remplaces \frac{1}{v_n} dans la partie droite. Ca donne e^{\frac{1}{v_n}} \leq 1+e \times \frac{1}{v_n} Or, v_{n+1}-v_n = e^{u_{n+1}}- e^{u_n} = e^{u_n + \frac{1}{v_n}} - e^{u_n}= e^{u_n} \times (e^{\frac{1}{v_n}} -1}) . Donc v_{n+1}-v_n \l...
- 21 Mar 2016, 22:35
- Forum: ✯✎ Supérieur
- Sujet: Suites et équivalents
- Réponses: 8
- Vues: 502
Re: Suites et équivalents
Pour montrer que 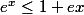 ?
?
- 21 Mar 2016, 22:26
- Forum: ✯✎ Supérieur
- Sujet: Suites et équivalents
- Réponses: 8
- Vues: 502
Re: Dériver une intégrale
Bonsoir, j'ai besoin de votre aide pour me lancer dans un exo. :? On me demande de dériver une 1ere fois puis une 2eme fois G(x). Avec G(x)= \int_{0}^x e^t ln(1+e^{-t}) \, \mathrm{d}t Et je ne connais pas la méthode. Et dans mon cours il n'y a pas d'exemples de ce type. Est-ce que je dois d...
- 21 Mar 2016, 22:15
- Forum: ✯✎ Supérieur
- Sujet: Dériver une intégrale
- Réponses: 2
- Vues: 1259
Re: Suites et équivalents
Bonsoir ! Tu peux utiliser le raisonnement par récurrence. D'abord, l'initialisation (qui est évidente). Puis, supposons u_n \geq \ln(n+1) . Alors e^{u_n} \geq n+1 , donc v_n \geq n+1 . Or, v_{n+1} \geq v_n +1 donc v_{n+1} \geq n+1+1 . En passant au logarithme, on obtient u_{n+1} \geq \ln...
- 21 Mar 2016, 22:11
- Forum: ✯✎ Supérieur
- Sujet: Suites et équivalents
- Réponses: 8
- Vues: 502
Bonjour, Je ne crois que l'auteur cherche à compliquer quoi que ce soit. Tu es dans le chapitre de fonctions trigonométriques, comme par exemple le développement en série de Fourier. Ces fonctions s'écrivent comme une somme (en général infinie) de a_n \cos(nx) + b_n \sin(nx) . Le cal...
- 20 Nov 2015, 14:15
- Forum: ✯✎ Supérieur
- Sujet: Ou veut-il en arriver?
- Réponses: 1
- Vues: 528
L.A. a écrit:Oui, dans R tout ensemble minoré admet une borne inférieure, et dans le cas d'un fermé cette borne inférieure est atteinte, c'est donc le plus petit élément.
Parfait, merci beaucoup.
- 18 Sep 2015, 20:29
- Forum: ✯✎ Supérieur
- Sujet: Périodicité et série entière
- Réponses: 15
- Vues: 1838
Bonjour, D'accord, merci. Néanmoins, je me suis dit que si on prend les fonctions cos et sin définies sur R, alors il n'y a pas de plus petit élément à cette image réciproque, alors que ça reste l'image d'un fermé. Voilà en fait pourquoi je ne comprends pas (même si il est évident qu'on parle ici d...
- 18 Sep 2015, 14:40
- Forum: ✯✎ Supérieur
- Sujet: Périodicité et série entière
- Réponses: 15
- Vues: 1838
Bonsoir, oui je sais mais je dois respecter la méthode du proffesseur, c'est à dire multiplier par le conjuguer en bas, simplifier , et trouver l'argument Oui mais comme l'écrit robot , tu dois aussi connaître la méthode du "professeur" arg(\frac{z}{z'})=arg(z)-arg(...
- 17 Sep 2015, 21:14
- Forum: ✯✎ Supérieur
- Sujet: Calcul argument complexe
- Réponses: 15
- Vues: 968
Robot a écrit:Il est facile de trouver l'argument de. Il est aussi facile de trouver l'argument de
. On en déduit l'argument du quotient
.
Oui c'est mieux comme ça en plus, tu as raison :++:
- 17 Sep 2015, 21:11
- Forum: ✯✎ Supérieur
- Sujet: Calcul argument complexe
- Réponses: 15
- Vues: 968
En fait, tu as exactement : z = 2 \times (sin(\frac{\pi}{12}) - cos(\frac{\pi}{12})) qu'on peut réécrire : z = 2 \times (sin(\frac{11\pi}{12}) + cos(\frac{11\pi}{12})) pour avoir une forme ...+... et il faut se souvenir de cos(\frac{\pi}{2}-x) ...
- 17 Sep 2015, 21:10
- Forum: ✯✎ Supérieur
- Sujet: Calcul argument complexe
- Réponses: 15
- Vues: 968
bonsoir, j'aurais besoin d'une aide, en faite , je dois trouver le module et argument de : (2;)(3) -2i)/(;)(2) +i;)(2)) j'ai trouver le module égal a 2 et en simplifiant l'expression j'ai trouver : ((;)(6) - ;)(2))/2)-(i(;)(6) +;)(2))/2) , mais lorsque je veux trouver l'argument, je tombe dans des ...
- 17 Sep 2015, 20:58
- Forum: ✯✎ Supérieur
- Sujet: Calcul argument complexe
- Réponses: 15
- Vues: 968
Bonjour, ce n'est pas l'image par la fonction réciproque, c'est l'image réciproque (l'ensemble des antécédents de 0 par cos) qui est définie même si la fonction réciproque n'est pas définie, comme c'est le cas ici. Bonjour, D'accord, merci. Néanmoins, je me suis dit que si on prend les fonctions co...
- 17 Sep 2015, 19:29
- Forum: ✯✎ Supérieur
- Sujet: Périodicité et série entière
- Réponses: 15
- Vues: 1838
Eh bien, c'était bien "pire" dans ma mémoire. Merci à tous pour vos réponses. Merci Ben pour cette réponse très détaillée. Je vais la recopier, cette démonstration m'est très précieuse ! En relisant et recopiant la démonstration pour la mémoriser, je me pose une question. Quand tu parles ...
- 17 Sep 2015, 16:27
- Forum: ✯✎ Supérieur
- Sujet: Périodicité et série entière
- Réponses: 15
- Vues: 1838
Cauchy2010 a écrit:Pièce équilibrée ??? Non, puisque la prob d'avoir pile = p par hypothèse et qu'on ne fait aucune hypothèse sur la valeur de p ...
Oui oui je suis d'accord, sauf que le 1/2 sort d'où alors ?
- 04 Aoû 2015, 22:02
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 24
- Vues: 1371
Bonjour à tous, celà fait quelques temps que j'essaye de comprendre par moi même comment résoudre des équations différentielles de second ordre avec second membre ainsi qu'avec des conditions initiales. J'ai compris qu'il fallait d'abord résoudre l'équation homogène puis la particulière mais je n'y...
- 04 Aoû 2015, 18:44
- Forum: ✯✎ Supérieur
- Sujet: équations différentielles
- Réponses: 7
- Vues: 688
Déjà autant pour moi, car il faut multiplier par la proba du dernier événement : Car la probabilité d'avoir un pile à la fin avec k changements est : -> La probabilité d'avoir un pile à l'avant-dernier avec autant de changements et avoir un pile au dernier (proba = p) + -> La probabilité d'avoir un ...
- 04 Aoû 2015, 17:06
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 24
- Vues: 1371
ok c'est fait j'ai représenté à chaque fois 2 branches de probas respectives p et 1-p mais je ne vois pas comment en déduire l'égalité recherchée car il y a énormément de possibilités.... Ce que j'ai écrit au dessus se fait bien avec un arbre où tu pars des événements P(n-1) et F(n-1) qui peuvent d...
- 04 Aoû 2015, 16:43
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 24
- Vues: 1371
Bonjour, j'aimerais une aide dans la réalisation de cet exercice: Soit n un entier naturel (sauf 0). On lance n fois une pièce de monnaie pour laquelle la probabilité d'obtenir pile est p et face est 1-p. On note X_n le nombre de fois où la pièce a changé de côté au cours de cette expérience. Pour ...
- 04 Aoû 2015, 16:36
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 24
- Vues: 1371
A et B commutent et donc possèdent une base de trigonalisation commune. On peut du coup utiliser ces faits, après avoir montré comment se défaire des vap complexes) : Si a+b>0 Si a>=b>=0 alors on a naturellement a^n+b^n > 0 (un des deux termes est non nul, et les deux sont positifs). Si b 0 (même r...
- 30 Juin 2015, 22:27
- Forum: ✯✎ Supérieur
- Sujet: déterminant et matrice réelle
- Réponses: 9
- Vues: 907
Bonjour ou bonsoir, J'essaye de faire un exercice sur les déterminants, je pensais que je serai capable de trouver au moins quelques petits trucs, mais ça fait un bon moment que je bloque. Du coup j'aurai bien besoin d'un coup de main svp. --- Soient A et B deux matrices carrées réelles telles que ...
- 30 Juin 2015, 20:47
- Forum: ✯✎ Supérieur
- Sujet: déterminant et matrice réelle
- Réponses: 9
- Vues: 907
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
