Probabilités
25 messages
- Page 1 sur 2 - 1, 2
Probabilités
Bonjour, j'aimerais une aide dans la réalisation de cet exercice:
Soit n un entier naturel (sauf 0). On lance n fois une pièce de monnaie pour laquelle la probabilité d'obtenir pile est p et face est 1-p. On note X_n le nombre de fois où la pièce a changé de côté au cours de cette expérience. Pour tout i appartenant à [[1,n]], on note Pi l'événement " on obtient pile au i ième lancer" (resp face).
On suppose ici n>=3 et k appartient [[1,n-2]]. Montrer que l'on a :
P((X_n=k)etP_n)=1/2 [P((X_(n-1)=k)etP_(n-1) + P((X_(n-1)=k-1)etF_(n-1)]
Faut il utiliser la formule des probabilités totales ?
je ne vois pas comment retrouver cette expression
merci de votre aide !
Soit n un entier naturel (sauf 0). On lance n fois une pièce de monnaie pour laquelle la probabilité d'obtenir pile est p et face est 1-p. On note X_n le nombre de fois où la pièce a changé de côté au cours de cette expérience. Pour tout i appartenant à [[1,n]], on note Pi l'événement " on obtient pile au i ième lancer" (resp face).
On suppose ici n>=3 et k appartient [[1,n-2]]. Montrer que l'on a :
P((X_n=k)etP_n)=1/2 [P((X_(n-1)=k)etP_(n-1) + P((X_(n-1)=k-1)etF_(n-1)]
Faut il utiliser la formule des probabilités totales ?
je ne vois pas comment retrouver cette expression
merci de votre aide !
pluie2 a écrit:Bonjour, j'aimerais une aide dans la réalisation de cet exercice:
Soit n un entier naturel (sauf 0). On lance n fois une pièce de monnaie pour laquelle la probabilité d'obtenir pile est p et face est 1-p. On note X_n le nombre de fois où la pièce a changé de côté au cours de cette expérience. Pour tout i appartenant à [[1,n]], on note Pi l'événement " on obtient pile au i ième lancer" (resp face).
On suppose ici n>=3 et k appartient [[1,n-2]]. Montrer que l'on a :
P((X_n=k)etP_n)=1/2 [P((X_(n-1)=k)etP_(n-1) + P((X_(n-1)=k-1)etF_(n-1)]
Faut il utiliser la formule des probabilités totales ?
je ne vois pas comment retrouver cette expression
merci de votre aide !
Salut !
Pour bien réécrire, ce que tu veux montrer est bien :
C'est étrange, car ça semble venir effectivement des probabilités totales... mais pour le 1/2 ?
Donc ce serait plutôt :
Car la probabilité d'avoir un pile à la fin avec k changements est :
-> La probabilité d'avoir un pile à l'avant-dernier avec autant de changements
+
-> La probabilité d'avoir un face à l'avant-dernier avec un changement de moins (pour avoir un pile à la fin).
(on ne peut pas avoir un changement de plus, sinon le nombre de changements devient supérieur à k, ce qui n'est pas possible).
pluie2 a écrit:ok c'est fait j'ai représenté à chaque fois 2 branches de probas respectives p et 1-p mais je ne vois pas comment en déduire l'égalité recherchée car il y a énormément de possibilités....
Ce que j'ai écrit au dessus se fait bien avec un arbre où tu pars des événements P(n-1) et F(n-1) qui peuvent donner ou Pn ou Fn.
Déjà autant pour moi, car il faut multiplier par la proba du dernier événement :
Car la probabilité d'avoir un pile à la fin avec k changements est :
-> La probabilité d'avoir un pile à l'avant-dernier avec autant de changements et avoir un pile au dernier (proba = p)
+
-> La probabilité d'avoir un face à l'avant-dernier avec un changement de moins et avoir un pile sur le dernier (proba = p aussi).
(on ne peut pas avoir un changement de plus, sinon le nombre de changements devient supérieur à k, ce qui n'est pas possible)
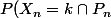= p \times P( X_{n-1}=k \cap P_{n-1}) + p \times P(X_{n-1}=k-1 \cap F_{n-1}))
Donc ton 1/2 vient sûrement d'une pièce équilibrée...
Car en factorisant, on a le "p" devant...
Car la probabilité d'avoir un pile à la fin avec k changements est :
-> La probabilité d'avoir un pile à l'avant-dernier avec autant de changements et avoir un pile au dernier (proba = p)
+
-> La probabilité d'avoir un face à l'avant-dernier avec un changement de moins et avoir un pile sur le dernier (proba = p aussi).
(on ne peut pas avoir un changement de plus, sinon le nombre de changements devient supérieur à k, ce qui n'est pas possible)
Donc ton 1/2 vient sûrement d'une pièce équilibrée...
Car en factorisant, on a le "p" devant...
pluie2 a écrit:on recherche alors la probabilité, pour 3 lancers, que la pièce ait changé 1 fois de côté et que pile soit obtenu au TROISIEME lancer soit :
je pose f=1-p
p*p*p+p*p*f+p*f*f+p*f*p comme proba.
Ta proba est fausse car p*p*p => k=0 et p*f*p => k=2 ... Or on impose k=1.
Comprends-tu bien tout ce que tu lis et fais ?!? :hum:
Si on commence par pile, on a comme indique zigomatique, mais on peut aussi commencer par face.
Donc ...
pluie2 a écrit:j'ai écrit et réfléchis trop vite mais j'ai bien compris pour l'exemple oui
donc il faut ajouter ce qui commence par face de façon à toujours avoir pile au troisième lancer OK
et donc tu observeras que seules les séquences qui commencent par face conviennent, puisque la contrainte est k=1. Confronte tes résultats à la formule générale.
Ensuite, si tu peux, tu regardes n=4 et k=1 puis 2 et tu essaies de voir si ça colle avec la formule générale. Tu devrais alors pouvoir conclure.
Bon courage et réfléchis bien avant :lol3:
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
