Calcul argument complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
weego
- Messages: 3
- Enregistré le: 17 Sep 2015, 20:27
-
 par weego » 17 Sep 2015, 20:38
par weego » 17 Sep 2015, 20:38
bonsoir,
j'aurais besoin d'une aide, en faite , je dois trouver le module et argument de :
(2;)(3) -2i)/(;)(2) +i;)(2))
j'ai trouver le module égal a 2 et en simplifiant l'expression j'ai trouver :
((;)(6) -

(2))/2)-(i(;)(6) +;)(2))/2)
, mais lorsque je veux trouver l'argument, je tombe dans des calcul avec des racine carré qui n'arrange pas la chose, y'aurait-il une méthode simple pour avoir une meilleur simplification ?
Merci d'avance
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 17 Sep 2015, 20:58
par BiancoAngelo » 17 Sep 2015, 20:58
weego a écrit:bonsoir,
j'aurais besoin d'une aide, en faite , je dois trouver le module et argument de :
(2;)(3) -2i)/(;)(2) +i;)(2))
j'ai trouver le module égal a 2 et en simplifiant l'expression j'ai trouver :
((;)(6) -

(2))/2)-(i(;)(6) +;)(2))/2)
, mais lorsque je veux trouver l'argument, je tombe dans des calcul avec des racine carré qui n'arrange pas la chose, y'aurait-il une méthode simple pour avoir une meilleur simplification ?
Merci d'avance
Bonsoir,
Ce que tu as écrit est bien.
C'est simplement parce que tu ne connais pas les valeurs de cos(pi/12) et sin(pi/12) qui vont t'aiguiller !
-
Robot
 par Robot » 17 Sep 2015, 21:08
par Robot » 17 Sep 2015, 21:08
Il est facile de trouver l'argument de
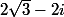
. Il est aussi facile de trouver l'argument de
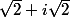
. On en déduit l'argument du quotient
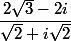
.
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 17 Sep 2015, 21:10
par BiancoAngelo » 17 Sep 2015, 21:10
En fait, tu as exactement :
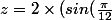 - cos(\frac{\pi}{12})))
qu'on peut réécrire :
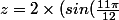 + cos(\frac{11\pi}{12})))
pour avoir une forme ...+...
et il faut se souvenir de
 = sin(x))
et idem en
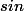
.
Donc un argument va être

qui donne:
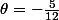
On a bien :
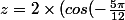 + sin(-\frac{5\pi}{12})))
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 17 Sep 2015, 21:11
par BiancoAngelo » 17 Sep 2015, 21:11
Robot a écrit:Il est facile de trouver l'argument de
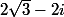
. Il est aussi facile de trouver l'argument de
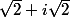
. On en déduit l'argument du quotient
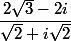
.
Oui c'est mieux comme ça en plus, tu as raison :++:
-
weego
- Messages: 3
- Enregistré le: 17 Sep 2015, 20:27
-
 par weego » 17 Sep 2015, 21:12
par weego » 17 Sep 2015, 21:12
Bonsoir, oui je sais mais je dois respecter la méthode du proffesseur, c'est à dire multiplier par le conjuguer en bas, simplifier , et trouver l'argument
-
alphamethyste
- Membre Relatif
- Messages: 290
- Enregistré le: 01 Mai 2015, 06:06
-
 par alphamethyste » 17 Sep 2015, 21:13
par alphamethyste » 17 Sep 2015, 21:13
salut
(2;)(3) -2i)/(;)(2) +i;)(2))
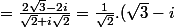.(1-i))
il faut utiliser le produit du complexe par son conjugué dans l'expression de l'inverse d'un complexe
c'est déjà plus facile
en effet
^2=(1+i).\overline {1+i}=(1+i)(1-i)=2)
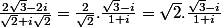
or
^2}-i\frac {1}{(\sqrt {1^2+1^2})^2}=\frac {1}{2}-i\frac {1}{2}=\frac {1}{2}(1-i))
donc du coup (2;)(3) -2i)/(;)(2) +i;)(2)) =
.\frac {1}{2}(1-i)=\frac {1}{\sqrt {2}}.(\sqrt {3}-i).(1-i))
-
Robot
 par Robot » 17 Sep 2015, 21:13
par Robot » 17 Sep 2015, 21:13
C'est idiot !
Ton professeur ne t'a pas appris que l'argument d'un produit (resp. quotient) est la somme (resp. différence) des arguments ?
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 17 Sep 2015, 21:14
par BiancoAngelo » 17 Sep 2015, 21:14
weego a écrit:Bonsoir, oui je sais mais je dois respecter la méthode du proffesseur, c'est à dire multiplier par le conjuguer en bas, simplifier , et trouver l'argument
Oui mais comme l'écrit
robot , tu dois aussi connaître la méthode du "professeur"
=arg(z)-arg(z'))
!
-
weego
- Messages: 3
- Enregistré le: 17 Sep 2015, 20:27
-
 par weego » 17 Sep 2015, 21:28
par weego » 17 Sep 2015, 21:28
Oui merci beaucoup, vous aviez raison,ca marche aussi et c'est simple bonne soirée à vous
-
Robot
 par Robot » 17 Sep 2015, 22:10
par Robot » 17 Sep 2015, 22:10
Avec plaisir.
 par marius firmin » 21 Sep 2015, 15:19
par marius firmin » 21 Sep 2015, 15:19
Bonsoir à tous .
Svp j'aimerai savoir comment faire pour
Calculer : log(i)
Merci d'avance pour vos reponses.
-
Robot
 par Robot » 21 Sep 2015, 15:25
par Robot » 21 Sep 2015, 15:25
Pose ta question sur un nouveau fil. Ca ne se fait pas de squatter un vieux fil avec une question différente.
 par marius firmin » 21 Sep 2015, 15:33
par marius firmin » 21 Sep 2015, 15:33
Bonsoir ,
Svp j'ai besoin d'aide pour calculer le nombre
Complexe : (i)^(i) .
Merci d'avance.
 par marius firmin » 21 Sep 2015, 15:45
par marius firmin » 21 Sep 2015, 15:45
Bonsoir , svp
j'aimerai qu'on m'aide à exprimer
un argument du nombre complexe : ( 2 + 3(x-iy) )
en fonction de A sachant que Z a pour argument A
et que Z=x+iy.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 21 Sep 2015, 16:10
par Sylviel » 21 Sep 2015, 16:10
Comme déjà dis plus haut : pose ta ou tes questions sur un nouveau fil.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
