Forum de Mathématiques: Maths-Forum

Ou encore dire que B est diagonalisable et pas A.

Joker62 a écrit:- Les deux matrices proposées sont sous la forme réduite de Jordan

...sauf la deuxième.
Mais si tu regardes les rangs de A-I et de B-I tu as la réponse.

On ne peut pas trouver de primitive qui s'exprime avec les fonctions usuelles.

c=3a et a=OA=OF+FA=c+1 donc tu trouves c, puis O puis A' ainsi que b , B et B'.

En effet, si on écrit , le PGCD de a et b' est aussi le PGCD de a et b donc c'est 1.
On peut aussi prendre pour le cas où ce serait 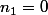qui donne le nombre premier.

Merci.

A la réflexion, ça pourrait être équivalent au théorème de Dirichlet. Car s'il existe un nombre premier dans toute suite arithmétique convenable, on doit pouvoir en trouver un deuxième dans une sous-suite en choisissant bien k. Puis réitérer le truc.
A voir...

Bonjour.

Il est difficile de montrer qu'il y a une infinité de nombres premiers dans la suite (a et b étant des entiers premiers entre eux donnés).
Mais y-a-il une raison simple pour que cette suite contienne au moins un nombre premier?

Si quelqu'un a une idée...

Primality a écrit: le point A est forcément entre K et F ?

oui, c'est le sommet de droite.

En posant tu as et .
Tu as aussi, en notant K le point d'intersection de D et de l'axe focal, .

est solution de l'équation de Pell dont la résolution est classique.

barbu23 a écrit:Il suffit de prendre l'élément : qui est d'ordre , car tu as dis que divise . :happy3:

C'est bien ça le bon argument et pas celui de Mohamed.
Le théorème de Cauchy est plus compliqué et inutile ici.

Pour prolonger une liste de longueur n+1 , tu as une ou deux façons selon que ta liste se termine par PP, FF ou plutôt PF, FP. D'où u_{n+2}=u_{n+1}+d_n où d_n est le nombre de listes de longueur n+1 qui se prolongent de deux manières. L'ensemble de ces dernières listes est en bijection avec l'ensemb...

Bonjour, Dans ce genre d'anneau, on a souvent une application "norme" N : A\rightarrow \mathbb Z . Ici c'est N(a+b\sqrt{-5})=a^2+5b^2 . La norme est multiplicative : N(uv)=N(u)N(v) . Par suite, si uv=1, alors N(u)=N(v)=\pm 1 et on peut avancer.

On peut généraliser :
avec injective surjective) .

momokani a écrit:montrer que quel que soit k entre 1 et p
1+4k n'est pas un carré parfait modulo p

Pourtant, avec k=2...

J'ai pas fait les calculs mais l'intégrale sur le contour C_b et l'intégrale sur [-b,b], c'est de toute façon pas la même chose. Il n'y a que pour b infini que ça coïncide à cause du lemme de Jordan qui te dit que l'intégrale sur le demi-cercle tend vers 0. La méthode sans les résidus me parait bien...

Le théorème des résidus, et plus généralement une intégrale curviligne, exige qu'il y ait pas de pôle sur le contour. Si on appelle F(b) l'intégrale sur le demi-cercle de rayon b que tu évoques, F(b) passe de 0 (lorsque b<a) à une valeur >0 et indépendante de b (lorsque b>a), bref F est pas prolonge...

ey74 a écrit:Dans quel cas une extension simple k(x)={(P/Q)(x)|P,Q dans k[X], Q(x) non nul} sur un corps k peut - elle s'exprimer ainsi:
k(x)={ax+b| a,b dans k}

Quand elle est de degré 1 ou 2 sur k.

et si (E est la partie entière).

Cette fonction est continue et même dérivable en 0. Elle n'est C° sur aucun voisinage de 0.

Vlad-Drac a écrit:donc on sait que ker(u*) = l'orthogonal de im(u)
ker(-u) = l'orthogonal de im(u)
voila je ne vois pas quoi faire apres

ke(-u)=ker(u) donc tu as gagné.