Equation avec entiers ...

[NBK59]

Bonjour,

Je cherche à trouver les couples d'entiers (N,n) avec N>=n qui répondent à :

N²+N =2(n²-n)

Mis à part calculer le Delta de l'équation du second degré, qui me donne

1+8(n²-n) et qui doit être un carré ...

Je ne vois de piste ....

[alm]

Bonjour :

Bonjour,

Je cherche à trouver les couples d'entiers (N,n) avec N>=n qui répondent à :

N²+N =2(n²-n)

Mis à part calculer le Delta de l'équation du second degré, qui me donne

1+8(n²-n) et qui doit être un carré ...

Je ne vois de piste ....

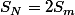J'essaye de chercher à travers la remarque : en posant pour tout entier naturle non nul , ton équation devient et 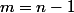mais je ne sais pas si je vais arriver à la résoudre comme ça

[yos]

est solution de l'équation de Pell dont la résolution est classique.

[chan79]

est solution de l'équation de Pell dont la résolution est classique.

oui, on est amené à élever à des puissances impaires (1+ )
Quelques exemples


N=(7-1)/2=3
n=(5+1)/2=3
d'où la solution (N,n)=(3,3)

N=(41-1)/2=20
n=(29+1)/2=15
d'où la solution (N,n)=(20,15)


N=(239-1)/2=119
n=(169+1)/2=85
d'où la solution (N,n)=(119,85)
etc