Probabilité - pièce et séquence de trois elements consécutifs égaux

[RoMz34]

Bonjour,

Je rencontre quelques petits problème dans la résolution d'un exo, mais c'est surtout un problème de méthode.

Voici l'énoncé :

On lance successivement et de façon indépendante une pièce équilibrée et on s'intéresse aux listes Pile ou Face comportant trois élements consécutifs égaux. (càd séquence du type (P,P,P) , (F,F,F))

On note En l'évenement "il y a apparition d'au moins 3 côtés consécutifs égaux lors des n 1ers lancers" et Rn son évenement contraire. De plus, on note Un le nombre de n-listes d'élements {P,F} ne comportant pas trois éléments consécutifs égaux.

1) Justifier que U1 = 2, u2 = 4 et u3 = 6. Calculer u4.

Ici, je ne trouve pas de méthode calculatoire ...

Je note O l'ensemble des solutions, et je dit de card(O) = 2^n (n l'indice Un).
Ensuite, j'exclut les solution avec au moins 3 pile ou 3 faces consécutifs.

Pour u1 -> O(P,F) donc u1 = 2
Pour u2 -> card(O) = 2^2 = 4 et zero (F,F,F) ou (P,P,P) donc u2 = 4
Pour u3 -> Card(O) = 2^3 = 8 et on a (PPP, FFF) donc u3 = 8 - 2 = 6
Pour u4 -> card(O) = 2^4 = 16 avec (PPPP, FFFF, PPPF, FPPP, PFFF, FFFP) câd u4 = 16 - 6 = 10

Je peut faire aussi des arbre, mais il n'y a rien de purement calculatoire ? (en même temps, c'est des probas).



2) Soit n entier naturel non nul.

2.1) Justifier que le nombre de (n+2) - liste de Rn+2 commençant par PF ou FP est égale à Un+1


Voila ou je bloque réellement. j'ai mis ça :

En commençant par PF ou FP, le 1er lancé est exclut de tout triplet possible, donc l'evenement En est indépendant du 1er lancé. Son contraire Rn est donc également indépendant du 1er lancé.
Cet expérience nous ramène donc à l'étude de n+1 lancers indépendant, càd que le nombre de (n+2)-listes de Rn+2 est égale à Un+1.

En fait, c'est évident, mais n'y a-t-il pas de moyen de justifier ça de manière plus mathématiques ?

[RoMz34]

Personne ? ...

[yos]

Pour prolonger une liste de longueur , tu as une ou deux façons selon que ta liste se termine par PP, FF ou plutôt PF, FP.
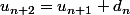D'où où 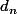est le nombre de listes de longueur n+1 qui se prolongent de deux manières. L'ensemble de ces dernières listes est en bijection avec l'ensemble des listes de longueur n (la (n+1)-ème coordonnée étant déterminée par la n-ème)

Tu dois donc avoir .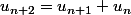

Quant à la question 1, il faut bien sûr raisonner par exhaustion. Il ne faut pas confondre calcul et magie.

[RoMz34]

Pour prolonger une liste de longueur , tu as une ou deux façons selon que ta liste se termine par PP, FF ou plutôt PF, FP.
D'où où est le nombre de listes de longueur n+1 qui se prolongent de deux manières. L'ensemble de ces dernières listes est en bijection avec l'ensemble des listes de longueur n (la (n+1)-ème coordonnée étant déterminée par la n-ème)

Tu dois donc avoir .

Quant à la question 1, il faut bien sûr raisonner par exhaustion. Il ne faut pas confondre calcul et magie.

Merci, il est vrai qu'en plaçant le PF, ou FP à la fin, la réponse devient plus évidente.