Une proposition de solution , en espérant ne pas m'être trompé avec toutes ces inégalités ( je n'utilise pas de trinôme non plus ) . Je pensais , j'espère à tort , que la fin ne marchait pas quand a , b et c étaient simultanément négatifs mais en fait il n'en est rien .
A/ On se place d'abord dans le cas a=c , il faut montrer que :si
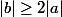
,
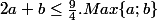
.
1°) Si
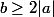
alors
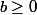
et
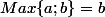
:
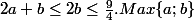
.
2°) Si
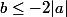
alors
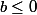
.
a) Si
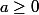
:
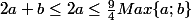
.
b) Si
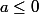
alors
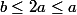
et
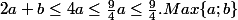
.
La propriété est donc établie dans tous les cas .
B/ Plaçons-nous maintenant dans le cas général , a , b , c donnés avec
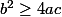
et montrons que :
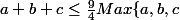
Remarquons tout d'abord que pour tous réels
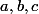
:
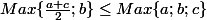
.
Comme
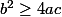
,
^2-(a-c)^2\geq (a+c)^2)
donc
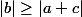
. On peut donc appliquer la partie A/ à

et
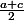
:
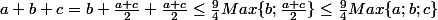
.
Imod

