C'est un programme qui me donne la "factorisation".
A la main ça doit être faisable de le trouver mais c'est long et faut pas se gourrer (l'espace des polynomes de degré 5 invariants est de dimension 7, on a juste 13 polynômes homogènes de degré 5 positifs à calculer, qu'il faut ensuite additionner entre eux pour trouver le polynôme de départ, et au final il en faut que deux alors bon...)
Petite inégalité qui me casse la tête ...
25 messages
- Page 2 sur 2 - 1, 2
soit un reel positif
un reel positif
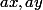 et
et 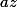 veriefient les hypotheses et l'inegalité.
veriefient les hypotheses et l'inegalité.
on peut donc choisir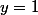 ,
, 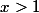 et
et 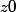
=2x/z - z/x^2 + z^2 - 2x = 2x(1/z - 1) -z/x^2 + z^2)
tous les termes de la somme sont des fonctions croissantes en x; il suffit donc pour verifier sa positivité de la regarder pour
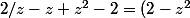(1-z)/z>0)
donc est croissante sur [1,inf[
est croissante sur [1,inf[
il ne reste plus qu'a verifier l'inegalité de depart avec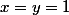
soit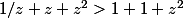
c'est à dire
^2/z>0)
cqfd
ps
les inegalité sont larges.
on peut donc choisir
tous les termes de la somme sont des fonctions croissantes en x; il suffit donc pour verifier sa positivité de la regarder pour
donc
il ne reste plus qu'a verifier l'inegalité de depart avec
soit
c'est à dire
cqfd
ps
les inegalité sont larges.
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
