Inégalité - Factorielle

[egan]

Résoudre dans :

Ou plus généralement, tu peux essayer aussi : , avec et des naturel premiers.

Zweig, tu aurais une petite piste pour ça ?

[Zweig]

Pas de soucis. Je te donne l'aide pour la généralisation. J'ai oublié de préciser

i) et peuvent-ils être impairs simultanément ? Que peux-tu en déduire sur la valeur de l'un d'eux ? (rappel : ils sont premiers)

ii) Montre par une disjonction de cas que et doivent nécessairement être de parité contraire.

Il reste encore des choses, mais fais déjà ça, et après vois comment tu peux continuer.

Une dernière chose : l'identité par excellence à utiliser dans toute la démonstration :

[egan]

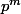
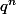
Si p et q étaient impaires simultanément, alors et seraient impaires simultanément. Or la différence de deux nombres impaires est un nombre paire. Comme 1 est impaire, p et q ne peuvent être impaires simultanément.
Donc on doit avoir soit p paire et q impaire, soit p impaire et q paire.
L'équation de départ revient à ça:
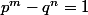
ou
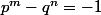
Si l'on traite le premier cas (on traiterait le second par un raisonnement analogue), on aurait que p doit être impaire et que q doit être paire.
Or p et q sont des nombres premiers et le seul nombre premier paire est 2.
Donc p est un nombre premier quelconque et q=2.

Supposons que m et n soient simultanément paires. On pose m=2k et n=2k' avec k et k' entiers naturels non nuls.
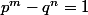
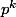
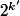
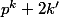
L'équation devient alors . Les deux facteurs de ce produit étant des entiers naturels, ils sont tous les deux égaux à 1. Or est supérieur strictement à 1 et de même pour . Donc le facteur ne peut être égal à 1 donc m et n ne peuvent pas être simultanément paires.
Dans le cas où m et n seraient simultanément impaires, en posant m=2k+1 et n=2k'+1 avec k et k' entiers naturels non nuls, en raisonnement de même et en utilisant la relation que tu as donné, on montrerait que l'un des termes ne peut pas être égal à 1.

Ca vous paraît juste ?
Reste la suite maintenant. Faut que je réfléchisse un peu. ^^

[egan]

Oula en fait non, erreur de ma part sur le cas où m et n sont simultanément impaires. J'ai pas trouvé encore.
Je ne vois vraimant pas comment montrer qu'ils ne peuvent pas être simultanément impaires.

[kasmath]

salut
[img]http://latex.codecogs.com/gif.latex?n!&space;+&space;n&space;=&space;(n!-1)&space;\times&space;1&space;+&space;(n+1)&space;\ge&space;n!\sqrt[n!]{\underbrace{1\cdot&space;1\cdot&space;1&space;\cdots&space;1}_{n-1}\cdot&space;(n+1)}[/img]
et



alors
[img]http://latex.codecogs.com/gif.latex?\frac&space;{1}{\sqrt&space;[n!]{n&space;+&space;1}}&space;+&space;\frac&space;{1}{\sqrt&space;[n]{n!&space;+&space;1}}\geq\frac&space;{n!}{n!&space;+&space;n}&space;+&space;\frac&space;{n}{n!&space;+&space;n}&space;=&space;1[/img]


[img]http://latex.codecogs.com/gif.latex?n^{n-1}=\underbrace{n\cdot&space;n\cdot&space;n&space;\cdots&space;n}_{n-1}&space;\ge&space;2\cdot&space;3\cdots&space;n&space;=&space;n![/img]

[kasmath]

[CENTER][img][IMG]http://latex.codecogs.com/gif.latex?n!&space;+&space;n&space;=&space;(n!-1)&space;\times&space;1&space;+&space;(n+1)&space;\ge&space;n!\sqrt[n!]{\underbrace{1\cdot&space;1\cdot&space;1&space;\cdots&space;1}_{n-1}\cdot&space;(n+1)}[/img]
[/IMG]



[img]http://latex.codecogs.com/gif.latex?n!+n&space;\ge&space;n\sqrt[n]{(n!+1)\cdot&space;\underbrace{1\cdots&space;1}_{n-1}}[/img]


[img]http://latex.codecogs.com/gif.latex?\frac&space;{1}{\sqrt&space;[n!]{n&space;+&space;1}}&space;+&space;\frac&space;{1}{\sqrt&space;[n]{n!&space;+&space;1}}\geq\frac&space;{n!}{n!&space;+&space;n}&space;+&space;\frac&space;{n}{n!&space;+&space;n}&space;=&space;1[/img][/CENTER]

:

[CENTER][img]http://latex.codecogs.com/gif.latex?n^{n-1}=\underbrace{n\cdot&space;n\cdot&space;n&space;\cdots&space;n}_{n-1}&space;\ge&space;2\cdot&space;3\cdots&space;n&space;=&space;n![/img][/CENTER]

:

[RIGHT][CENTER][img]http://latex.codecogs.com/gif.latex?\frac&space;{n!}{n^{n-1}}&space;\le&space;\frac{n!}{n!}&space;=&space;1[/img][/CENTER][/RIGHT]

.[/COLOR][/SIZE][/FONT]

[egan]

Vous devez certainement avoir une idée. Un tit coup de pouce pour le pauvre malheureu que je suis ? ^^