Inégalité

[Zweig]

Bonjour, je suis nouveau.

La factorisation est vraiment puissante (tu l'as trouvé sur le coup Zweig?), d'un autre côté ça me chagrine de ne pas pouvoir compléter le raisonnement de Lapras pour a, b et c négatifs...
Ca doit pouvoir se faire, j'essaye.

Non, cette réécriture n'est pas de moi. Je l'avais trouvée il y'a quelques temps sur le Net.

[Mhdi]

Donc, on peut supposer que a+b+c=0 ?
Question de ne pas partir du mauvais côté..

[Zweig]

Oui :id: :id:

[Mhdi]

Ah! autre chose (-_-) : si une inégalité est homogène, peut-on poser deux contraintes en même temps? genre a+b+c=0 et abc=1

[Zweig]

Bonne question !

[Mhdi]

Bonne question !

...A laquelle tu as une réponse? :we:

[Zweig]

Non, sinon je t'aurais répondu :we:

[lapras]

Je pense qu'on peut avoir les contraintes :
abc = u
et
a+b+c = v
en même temps car elles ne suffisent pas à déterminer les variables, c'est a dire les contraintes ne sont pas trop fortes...

[Mhdi]

En fait je pense que non :
Si je prend pour exemple l'inégalité précédente et que je pose :
On remarque que f(ka,kb,kc)=f(a,b,c) donc on peut remplacer a b et c par ka kb et kc (k £ R). Ensuite on pose . Puis on choisit , ce qui nous donne a'+b'+c'=1. mais maintenant que k est fixée, on ne peut plus donner une valeur quelconque à a'b'c', car

C'est peut-être faux, mais c'est en tout cas ce que je pense

[ThSQ]

Ah! autre chose (-_-) : si une inégalité est homogène, peut-on poser deux contraintes en même temps? genre a+b+c=0 et abc=1

En général non.

[mehack]

C'est vrai que certaines inégalités peuvent être résolues d'une manière très habile ... comme celle-ci :

Pour tous réels deux à deux différents, on a

sans trop reflechir on peut remarquer que :
qqs de R
la somme nous assure le resultat

[mehack]

slt !!
deux contraintes à la fois ca veut dire qu on est plus dans le cas general , donc quand une inegalité est homogeine on ne peut supposer qu une seule contrainte. par exemple si on suppose que abc=1 et a+b+c=3 on aura si peux de reels positifs qui satisfaitent ces deux contraintes , dans ce cas je crois qu il n y a qu une seul solution c est (a,b,c)=(1,1,1).
meme chose pour la symetrie si on suppose que a>=b>=c on peut pas supposer que a= :happy2:

[Khue]

Bonjour,

Je trouve qu'il y a des questions très intéressantes dans cette discussion. Je vais donner quelques idées, j'espère que qui vous satisfient.

Ah! autre chose (-_-) : si une inégalité est homogène, peut-on poser deux contraintes en même temps? genre a+b+c=0 et abc=1

Pour répondre à cette question, il faut tout d'abord répondre à la question: pour quoi dans les inégalités homogènes, on peut poser une contrainte parmi les variables ?
Notons que la question n'est pas exacte, car ce n'est pas toujours vrai. Dans la pluparts des livres d'inégalité, cette question n'est pas répondue justement.
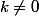
On rappelle la définition d'une fonction (ou expression) homogène: est dite homogène de degré ssi pour tout on a
.
Maintenant, considérons une inégalité sous la forme

avec et homogène de degré d.
Pour que l'on peut poser une contrainte , il faut 3 conditions suivantes:
1. doit être homogène de degré avec
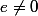
2. Tous les éléments de l'ensemble des valeurs de ont le même sige qui est non-nul.
3. est un élément de .

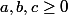
Par exemple, pour montrer une inégalité avec ; on ne meut pas supposer une des conditions suivantes:
1.
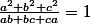
2.
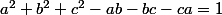
3.

Je vais montrer que l'on peut poser avec 3 conditions précédentes.
Supposons avec .
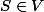
Poser
Alors on a
.
L'inégalité peut s'écrire

où
.

Maintenant on a et on doit montrer
Ca explique pourquoi on peut supposer .

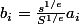
(Notons qu'il manque une condition pour que après changer variables , sont toujours dans le même ensemble de définition de , mais c'est assez compliqué, donc je n'ai pas ajouté dans la liste).

Un exemple: Prouver que

pour tous .
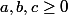
Dans ce cas là, on peut supposer que .
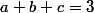
(Si a+b+c=k >0, on pose x=3a/k,y=3b/k,z=3c/k, alors on a x+y+z=3 et on doit montrer que f(x,y,z) \ge \frac{3}{5}).

Est-ce que c'est clair ?

[Zweig]

Je te remercie Khue :happy2: Très bonne explication que je cherchais depuis pas mal de temps !

Soient , et des réels positifs vérifiant. Déterminer le minimum de l'expression

Et pour les plus courageux :

Soient des réels positifs vérifiant et des constantes réelles positives. Déterminer pour tout entier naturel le minimum de l'expression

[ffpower]

Soit E l ensemble des (x1,..,xn) réels positifs tels que x1+...+xn=n.la fonction atteint son minimum sur E.Fixons un n uplet (x1,...,xn) ou un tel minimum est atteint.Si x1 et x2 sont tous 2 non nuls,pour t assez petit,(x1+t,x2-t,x3,....,xn) est dans E donc la fonction qui a t associe est minimale en t=0.En prenant la dérivée en 0 on obtient donc .De la meme maniere pour tout i,j,si xi et xj sont differents de 0,alors .Il existe donc une constante c telle que pour tout i,soit soit .En particulier donc en sommant .Il reste a déterminer c.Si ,on a pour tout i de I donc en sommant d'ou
Pour que c soit minimal,on doit avoir I=[1,n] et donc modulo etourderies le minimum vaut

[Zweig]

Ouep, bravo !

[Mhdi]

Hop!
Soit (a;b) £ R+ et a+b=1. Prouvez que:

[Zweig]

Hello,

L'inégalité à montrer se réécrit :



ou encore



qui se simplifie en



qui est une conséquence directe de l'inégalité arithmético-géométrique.

L'égalité est obtenue lorsque a = b = 0.5

[Mhdi]

Exact, c'est ce que j'avais fait. ;)
N'y a t-il pas possibilité de ne passer par le développement ?

[Zweig]

Aucune idée. Une autre méthode plus bourrine serait de substituer a par 1 - b et d'étudier un polynôme du second degré (après simplifications) ...