Inégalité
Olympiades mathématiques, énigmes et défis
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 08 Mai 2008, 13:09
par Mhdi » 08 Mai 2008, 13:09
Voici une inégalité facile, mais que j'ai trouvée très amusante :
Soit
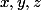
des réels positifs tels que:
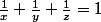
prouver que
(y-1)(z-1)>=8)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 08 Mai 2008, 13:39
par ThSQ » 08 Mai 2008, 13:39
Ca revient à
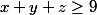
qui est Cauchy par exemple
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mai 2008, 13:53
par Zweig » 08 Mai 2008, 13:53
Salut Mhdi,
La contrainte se réécrit encore
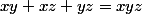
.
Le membre de gauche se réécrit quant à lui
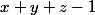
. L'inégalité à démontrer se résume alors à
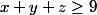
.
On pose
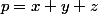
,
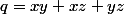
et
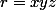
. L'inégalité de Schur s'énonce comme suit :
(a - c) + b^t(b - a)(b - c) + c^t(c - a)(c - b) \geq 0)
pour tout réel

.
En particulier, nous avons :
(a - c) + b^0(b - a)(b - c) + c^0(c - a)(c - b) \geq 0)
, qui se réécrit encore
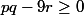
, ou encore
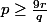
. Or
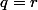
d'après la contrainte imposée par l'énoncé, d'où
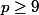
, comme désiré.
L'égalité est obtenue lorsque
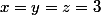
.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 08 Mai 2008, 15:18
par ThSQ » 08 Mai 2008, 15:18
Intéressante solution Zweig mais
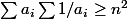
(Cauchy) est peut-être plus direct.
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 08 Mai 2008, 15:21
par Mhdi » 08 Mai 2008, 15:21
Salut,
J'ai bien aimé l'inégalité parce que j'ai réussi à la résoudre en n'utilisant aucune autre inégalité sauf la fameuse
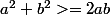 Ma solution:
Ma solution:démontrer que
(y-1)(z-1)>=8)
revient à démontrer que
(1-\frac{1}{y})(1-\frac{1}{z})>=8)
Et puisque
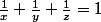
, il suffit de démontrer que
(\frac{1}{y}+\frac{1}{z})(\frac{1}{z}+\frac{1}{x})>=8)
On sait que :
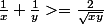
et
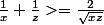
et
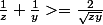
En multipliant, on obtient :
(\frac{1}{x}+\frac{1}{z})(\frac{1}{x}+\frac{1}{y})>=\frac{8}{xyz})
Ainsi,
(\frac{1}{y}+\frac{1}{z})(\frac{1}{z}+\frac{1}{x})>=8)
On conclut donc que
(y-1)(z-1)>=8)
@+
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 08 Mai 2008, 15:31
par ffpower » 08 Mai 2008, 15:31
Joli Mhdi..
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 08 Mai 2008, 15:35
par Mhdi » 08 Mai 2008, 15:35
Merci :happy2:
ThSQ>>Belle solution ;) ; l'efficacité de Cauchy-Schwarz :bad:
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 08 Mai 2008, 15:40
par Mhdi » 08 Mai 2008, 15:40
En voilà une plutôt difficile - je ne l'ai pas encore résolu !
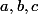
sont des réels strictement positifs tels que
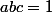
Démontrer que
(b+1)} + \frac{b}{(b+1)(c+1)} + \frac{c}{(c+1)(a+1)} >= \frac{3}{4})
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mai 2008, 16:08
par Zweig » 08 Mai 2008, 16:08
(b + 1)} + \frac {b}{(b + 1)(c + 1)} + \frac {c}{(c + 1)(a + 1)}\geq\frac {3}{4})
 + b(a + 1) + c(b + 1)]\geq3(a + 1)(b + 1)(c + 1))
(1)
En posant
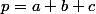
et
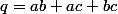
, l'inégalité à démontrer se réécrit :
\Leftrightarrow4(p + q)\geq3(p + q + 2)\Leftrightarrow p + q\geq6)
Or,
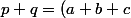 + (ab + ac + bc)\geq6\sqrt[6]{(abc)^{3}} = 6)
d'après l'inégalité arithmético-géométrique.
L'égalité est obtenue lorsque
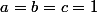
CQFD.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 08 Mai 2008, 16:10
par ThSQ » 08 Mai 2008, 16:10
Mhdi a écrit:En voilà une plutôt difficile
Jolie mais bêtement torchable par l'astuce a=x/y,b=y/z,c=z/x qui transforme en
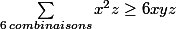
qui est l'inégalité entre moyennes.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mai 2008, 16:23
par Zweig » 08 Mai 2008, 16:23
J'en ai une relativement difficile.
Soient a, b, c des réels positifs et k un réel donné
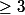
. Montrer l'inégalité suivante :
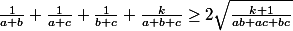
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 08 Mai 2008, 18:59
par lapras » 08 Mai 2008, 18:59
Bonsoir
j'arrive apres une bonne journée piscine, apres la bataille.
Je donne une solution que je viens de trouver
1/x + 1/y + 1/z = 1
<=>
xy + yz + zx = xyz
en développant (x-1)(y-1)(z-1) on obtient :
x+y+z >= 9
or
inégalité harmonique-arithmétique =>
(x+y+z)/9 >= 1/(1/x + 1/y + 1/z) = 1
=>
x+y+z >= 9
c'est donc fini
j'ai aussi trouvé une autre solution avec les moyennes arithmétiques et cauchy et réordonnement mais c'est beaucoup plus long.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 08 Mai 2008, 19:08
par ThSQ » 08 Mai 2008, 19:08
Intéressant, à noter que l'égalité n'a pas lieu quand a=b=c ce qui veut dire que les bazookas habituels vont être sans effet ici ....
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 08 Mai 2008, 19:23
par Zweig » 08 Mai 2008, 19:23
"les bazookas habituels" = inégalités classiques ?
Pas si sûr ... :we:
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 08 Mai 2008, 23:11
par Mhdi » 08 Mai 2008, 23:11
Elle est coriace la félonne :hum:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 09 Mai 2008, 07:08
par ThSQ » 09 Mai 2008, 07:08
Zweig a écrit:"les bazookas habituels" = inégalités classiques ?
Non c'est clair qu'il faudra utiliser une pièce du couteau suisse des inegs tôt ou tard. Je pensai plutôt aux astuces trivialisantes style homogénéisation, .....
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 09 Mai 2008, 11:37
par Zweig » 09 Mai 2008, 11:37
Perso, je n'ai pas eu besoin de ça, mais y'a peut-être une autre solution possible.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Mai 2008, 18:09
par Zweig » 10 Mai 2008, 18:09
Zweig a écrit:Soient a, b, c des réels positifs et k un réel donné
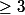
. Montrer l'inégalité suivante :
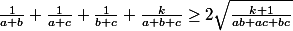
Personne n'a trouvé une solution ?
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 10 Mai 2008, 20:15
par Mhdi » 10 Mai 2008, 20:15
Un indice?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 10 Mai 2008, 20:38
par Zweig » 10 Mai 2008, 20:38
Bien sûr !
On pose p = a + b + c, q = ab + ac + bc, r = abc.
1) Trouvez une réécriture du membre de gauche en fonction de p, q et r (et k bien entendu).
2) La forme du membre de droite vous fait penser à quelle célèbre inégalité ? A partir de la réécriture du membre de gauche (et du membre de droite en fonction de k et q) et de la connaissance de la forme de cette célèbre inégalité , "bidouillez" pour démontrer l'inégalité en partant du membre de gauche.
"Tout" est dans le 1).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités