Bonsoir,
pour un programme de M1 similaire en analyse, le Brezis et le Hirsch-Lacombe m'ont été bien utile.
1512 résultats trouvés
Revenir à la recherche avancée
- 27 Avr 2010, 11:24
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme d'opérateur
- Réponses: 3
- Vues: 1024
- 27 Avr 2010, 10:41
- Forum: ✯✎ Supérieur
- Sujet: Isomorphisme d'opérateur
- Réponses: 3
- Vues: 1024
- 27 Avr 2010, 10:33
- Forum: ✯✎ Supérieur
- Sujet: (Topologie) Fermé dans RxR
- Réponses: 16
- Vues: 1804
Salut, de \frac{\partial{y}}{\partial{t}}=f( t,y(t)),\ y(t_{0})=y_{0} , tu obtiens l'expression suivante de y : y(t)=y_0+\int_{t_0}^t f(s,y(s)) ds , Donc si f est C^1 , y est C^2 . Pour la suite, on considère les applications F:\ t\rightarrow f(t,y...
- 27 Avr 2010, 09:39
- Forum: ✯✎ Supérieur
- Sujet: derivée de plusieurs variables
- Réponses: 2
- Vues: 602
Bonsoir,
je ne vois pas en quoi la question est mal posée.
Tu peux considérer par exemple une suite de parties de X telles que) , ou encore
, ou encore ) .
.
je ne vois pas en quoi la question est mal posée.
Tu peux considérer par exemple une suite de parties de X telles que
- 20 Mar 2010, 00:13
- Forum: ✯✎ Supérieur
- Sujet: Famille de parties de X contenant X
- Réponses: 5
- Vues: 916
- 17 Mar 2010, 21:00
- Forum: ✯✎ Supérieur
- Sujet: Intégrale généralisée
- Réponses: 6
- Vues: 762
Nightmare a écrit:L'ensemble des entiers relatifs muni de la topologie induite de R me semble convenir.
Les singletons forment une base d'ouverts pour la topologie et est dénombrable, non?
- 17 Mar 2010, 15:08
- Forum: ✯✎ Supérieur
- Sujet: Topologie (sic)
- Réponses: 30
- Vues: 1831
- 17 Mar 2010, 14:55
- Forum: ✯✎ Supérieur
- Sujet: Topologie (sic)
- Réponses: 30
- Vues: 1831
il faut chercher dans des espaces gros. Les fonctions définies sur [0,1] avec la convergence simple, il me semble que ça marche.
- 17 Mar 2010, 14:54
- Forum: ✯✎ Supérieur
- Sujet: Topologie (sic)
- Réponses: 30
- Vues: 1831
Salut Oui, pour un ensemble topologique là où la notion de suite est abscente, on la remplace par la notion de base de voisinages denombrables ! c'est quasi la même chose que ce qui se passe par rapport à un espace metrique, sauf qu'ici on remplace les elements par des sous ensembles ! donc, à toi d...
- 17 Mar 2010, 14:31
- Forum: ✯✎ Supérieur
- Sujet: Topologie (sic)
- Réponses: 30
- Vues: 1831
- 12 Fév 2010, 00:13
- Forum: ✯✎ Supérieur
- Sujet: DL d'une fonction par intégration
- Réponses: 4
- Vues: 729
- 11 Fév 2010, 23:23
- Forum: ✯✎ Supérieur
- Sujet: DL d'une fonction par intégration
- Réponses: 4
- Vues: 729
Bonsoir, Les vecteurs propres sont exactement les vecteurs de la forme (0,a,0), a\in \mathbb{R} . C'est un ev de dim 1. Donc on peut choisir n'importe lequel de ces vecteurs, l'espace propre sera le Vect du vecteur choisi. Le vecteur le plus simple est bien sur le meilleur choix. C'est celui proposé...
- 04 Fév 2010, 19:11
- Forum: ✯✎ Supérieur
- Sujet: Problèmes pour le calcul de vecteurs propres matrice 3x3
- Réponses: 4
- Vues: 3399
Pour compléter ce qu'a dit Ben314, la topologie *-faible \sigma(E',E) est la topologie faible \sigma(E',F) , où F=\textrm{im} J est un sous-espace vectoriel de E" , avec J:\ x\in E\rightarrow \varphi_x\in E" ( \varphi_x étant défini comme dans le post #5). Donc ici ...
- 23 Déc 2009, 14:07
- Forum: ✯✎ Supérieur
- Sujet: topologie faible
- Réponses: 15
- Vues: 2390
Pour chaque 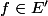 , tu montres que tout
, tu montres que tout ) -voisinage est un
-voisinage est un  -voisinage, et inversement.
-voisinage, et inversement.
Mais on peut se restreindre à parcourir des bases de voisinages en fait.
Mais on peut se restreindre à parcourir des bases de voisinages en fait.
- 22 Déc 2009, 23:38
- Forum: ✯✎ Supérieur
- Sujet: topologie faible
- Réponses: 15
- Vues: 2390
Une distance induit toujours une topologie, ici tu veux montrer que cette topologie est l'*-faible. En fait, le but de ton exo c'est de montrer que la topo *-faible est métrisable sur la boule unité de E', quand E est séparable (condition nécessaire voire suffisante?). La topo *-faible est plus pauv...
- 22 Déc 2009, 23:22
- Forum: ✯✎ Supérieur
- Sujet: topologie faible
- Réponses: 15
- Vues: 2390
Bonsoir, Ici il s'agit en fait de la topologie *-faible \sigma(E',E) , qui est la topologie la moins fine sur E' rendant les formes linéaires suivantes continues: à chaque x\in E , on associe la forme linéaire \varphi_x:\ f\in E'\rightarrow f(x) . Cherche le théorème de banac...
- 22 Déc 2009, 23:06
- Forum: ✯✎ Supérieur
- Sujet: topologie faible
- Réponses: 15
- Vues: 2390
Salut,
autre exemple illustrant la grosse perte de l'existence de base dans le cas des modules.
Tu prends un anneau A non principal, et un idéal I de A engendré par au moins deux éléments.
A est un A-module libre. Mais I est un A-module de type fini non libre.
autre exemple illustrant la grosse perte de l'existence de base dans le cas des modules.
Tu prends un anneau A non principal, et un idéal I de A engendré par au moins deux éléments.
A est un A-module libre. Mais I est un A-module de type fini non libre.
- 19 Déc 2009, 00:43
- Forum: ✯✎ Supérieur
- Sujet: Espace vectoriel
- Réponses: 9
- Vues: 698
Bonsoir, c'est peut être l'équation de Helmoltz: http://eqworld.ipmnet.ru/en/solutions/lpde/lpde303.pdf.
- 18 Déc 2009, 23:02
- Forum: ✯✎ Supérieur
- Sujet: equation de la chaleur
- Réponses: 21
- Vues: 2782
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
