Espace vectoriel

[barbu23]

Bonjour à tous :
Soit un anneau.
Soit une - algèbre.
Alors, par définition :
est anneau muni d'un homomorphisme d'anneau : .
Montrer que est un - module !
Merci de votre aide ! :happy3:

[Nightmare]

Je comprends pas, une A-algèbre n'est-elle pas en particulier un A-module (auquel on rajoute une loi) par définition?

[barbu23]

Oui, c'est ça ! merci ! et comment on exibe un système generateur au -module ?
J'ai une autre question à vous poser :
Est ce qu'il existe des modules qui n'ont pas de bases, ou au moins ils possèdent un système générateur mais qui ne sont pas libre ?
Merci d'avance ! :happy3:

[Ben314]

Quelle différence fait tu entre un -module et un -espace vectoriel ?
Si la réponse est "aucune", il y a un théorème dit "de la base incomplète" qui dit que (modulo l'axiome du choix) que....

[barbu23]

Quelle différence fait tu entre un -module et un -espace vectoriel ?

On me dit qu'il ny'a aucune difference ! mais, je ne suis pas trop convaincu ! :hum:
Ben314, que veut tu dire par :

il y a un théorème dit "de la base incomplète" qui dit que (modulo l'axiome du choix) que....

Je ne comprends pas bien cette phrase ! :hum:
Merci d'avance ! :happy3:

[barbu23]

Je connais le theorème de la base incomplète basée sur l'axiome de choix mais je ne comprends pas quel lien a avec la notion de modules ou ce que tu veux dire ! :happy3:

[Nightmare]

Le théorème de la base incomplète n'est plus vrai pour les modules, on a des modules qui n'ont pas de base. Par contre on a certains théorèmes qui assure l'existence d'une base pour certains modules (module libre par exemple si je ne me trompe pas)

[barbu23]

on a certains théorèmes qui assure l'existence d'une base pour certains modules

Oui, j'aimerai connaitre ces theorèmes là dont tu parles ! :happy3:
Merci de votre aide ! :happy3:

[Ben314]

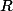
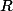
Personellement, vu les axiomes que je prend usuellement pour les e.v. et les A-modules (avec A unitaire), je ne fait pas de différence entre les deux quand A est en fait un corps. D'où ma réponse concernant les -modules qui, pour moi sont trés précisément des -espaces vectoriels donc admettent tous des bases...

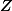
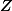
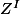
Par contre, si A n'est pas un corps, il peut évidement y avoir des A-modules sans bases. L'exemple le plus simple de A-modules (avec A non corps) est celui des -modules : ce sont en fait tout les groupes commutatif. Les -modules libres sont les groupes isomorphes à un pour un certain ensemble . Je pense que tu est capable de trouver tout seul un groupe commutatif qui ne soit pas un ...

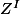
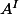
P.S. : Je sais pas si c'est clair dans ta tête : un A-module M est dit libre lorsqu'il admet une base, c'est à dire lorsqu'il est isomorphe à un pour un certain ensemble I.

[legeniedesalpages]

Salut,

autre exemple illustrant la grosse perte de l'existence de base dans le cas des modules.
Tu prends un anneau A non principal, et un idéal I de A engendré par au moins deux éléments.
A est un A-module libre. Mais I est un A-module de type fini non libre.