[Défi] Racines n-ième
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 02 Mai 2010, 18:36
par Zweig » 02 Mai 2010, 18:36
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 08:23
par benekire2 » 03 Mai 2010, 08:23
Salut Zweig,
Merci pour ce bel exo :zen:
Je rencontre des problèmes dans la quatrième question de la partie 3 ; je ne comprends pas vraiment ce que signifie nN
Après j'ai de gros soucis dans la partie 4 ; la 5 n'en parlons pas et la 6 non plus !!
Merci!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mai 2010, 10:33
par Ben314 » 03 Mai 2010, 10:33
Salut,
Pour le III)4), tu peut constater que

puis que ta somme est de la forme

(attention au cas particulier...)
[Remarque : dans cette somme, il vaudrait mieux prendre un indice pour la somme différent de i, vu que, dans
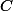
, la lettre i sert déjà...]
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 03 Mai 2010, 10:58
par Zweig » 03 Mai 2010, 10:58
Salut,

sont les multiples positifs de

(je ne sais pas comment faire en latex le | barré pour "non divisible", donc j'ai rusé ...)
Aussi,
|)
désigne le cardinal de
)
, càd le nombre d'éléments de l'ensemble
)
Ben > En effet, j'avais pas percuté quand j'ai rédigé le PDF ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 11:32
par benekire2 » 03 Mai 2010, 11:32
merci Zweig pour cette précision, pour le cardinal de phi(n) j'avais compris par contre.
Merci ben, je vais essayer ça tout à l'heure.
Une question pour la partie IV] :
Dois-je passer au module et utiliser la première partie ? ... Merci !!!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mai 2010, 11:52
par Ben314 » 03 Mai 2010, 11:52
"x \not | y" =>

Pour la partie 4, tu as effectivement intérêt à écrire en modules :
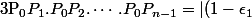(1-\epsilon_2)<br />\cdots(1-\epsilon_{n-1})|=...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 14:12
par benekire2 » 03 Mai 2010, 14:12
Ouais j'ai fait par les modules aussi , mais le problème c'est que j'arrive sur ... la deuxième relation à prouver, ce qui est complètement con ... y a une simplification que j'ai pas vue ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 03 Mai 2010, 16:08
par Zweig » 03 Mai 2010, 16:08
Yop,
Pour cette question, considère
 = z^n-1,\, z\in\mathbb{C})
. Calcule ensuite de deux manières différentes
|)
.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 03 Mai 2010, 16:11
par Zweig » 03 Mai 2010, 16:11
J'aurai pu rajouté aussi que les produits des

racines de l'unité vallent
^{n+1})
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 17:09
par benekire2 » 03 Mai 2010, 17:09
Zweig a écrit:Yop,
Pour cette question, considère
 = z^n-1,\, z\in\mathbb{C})
. Calcule ensuite de deux manières différentes
|)
.
Je suis pas sûr de te suivre ... mais si on considère que ça se dérive comme une fonction réelle on a f'(1)=n faudrait donc montrer que l'autre membre vaut f'(1) aussi en ces cas là.
Je remarque que ça se factorise par (z-1) mais c'est tout :triste:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 03 Mai 2010, 18:31
par Zweig » 03 Mai 2010, 18:31
Ah, tu fais bien de demander de l'aide pour cette question, j'ai oublié de préciser un résultat à admettre :
Si un polynôme de degré

admet

racines distinctes
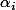
, alors il se factorise sous la forme
 = \lambda\prod^n_{i=1}(x-\alpha_i))
Grâce à une certaine partie du PDF, tu as toutes les racines de

et donc tu peux le factoriser.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mai 2010, 18:34
par Nightmare » 03 Mai 2010, 18:34
Salut,
ça manque de choses à propos de la structure de groupe de l'ensemble des racines n-ème, et en particulier une chose primordiale : sa cyclicité.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 18:45
par benekire2 » 03 Mai 2010, 18:45
oui toutes les racines de f sont les racines n-ièmes de l'unité.
Mais en fait j'ai pas l'impression que ça m'avance ... Je vais récapituler:
Je réécrit l'énoncé :
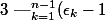|=n)
Et on a montré qu'avec
=z^n-1=\Bigprod_{k=0}^{n-1} (z-\epsilon_k))
on a
|=n)
il "suffit" donc de montrer que
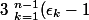=f'(1))
Et c'est précisément là que je n'y arrive plus...
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 03 Mai 2010, 18:48
par Zweig » 03 Mai 2010, 18:48
Non non, on a plutôt, d'après ma formule
 = \prod^{n-1}_{i=0}(z-\epsilon_i))
EDIT : Ok tu as edité avant ...
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 19:02
par benekire2 » 03 Mai 2010, 19:02
Zweig a écrit:Non non, on a plutôt, d'après ma formule
 = \prod^{n-1}_{i=0}(z-\epsilon_i))
EDIT : Ok tu as edité avant ...
Et oui :zen:
mais sinon c'est bien ça ? Je dois montrer que
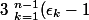=f'(1))
Si oui , comment m'y prendre, parce que je vois pas trop . Merci !!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mai 2010, 19:08
par Ben314 » 03 Mai 2010, 19:08
Bon, je te donne une "grosse" indic :
Partant de
=z^n-1=\Bigprod_{k=0}^{n-1} (z-\epsilon_k))
comment obtenir
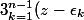)
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 19:27
par benekire2 » 03 Mai 2010, 19:27
ah , et bien il faut diviser par z-1
le problème étant que c'est le produit des z-1 pas des z-epsilon .

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mai 2010, 21:00
par Ben314 » 03 Mai 2010, 21:00
Tu as donc, pour tout complexe z différent de 1 :
)
Et si maintenant tu fait endre z vers 1...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 03 Mai 2010, 21:06
par benekire2 » 03 Mai 2010, 21:06
ok ... tu m'as eu ! Réécrit comme ça c'est tout de suite évident ! Merci :zen:
Ensuite pour l'application suivante, c'est pas trop compliqué ; par contre la dernière application géométrique on fait comment ? :hein:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Mai 2010, 21:14
par Ben314 » 03 Mai 2010, 21:14
Je sais pas si c'est ce qu'attend Zweig, mais si tu écrit la première formule trigo en prenant n=2m pair et que tu sépare le produit en deux :les k pairs d'un coté et les impair de l'autre alors...
Edit : avec la méthode qui me venait à l'esprit (ci dessus), j'obtient :
\pi}{2n}\right)=\frac{1}{2^{n-1}})
mais je pense qu'il y a une faute de frappe et que c'est bien ça qu'il faut montrer car le produit
\pi}{n}\right))
est nul lorsque n est impair, vu qu'il contient
=0)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
 puis que ta somme est de la forme
puis que ta somme est de la forme  (attention au cas particulier...)
(attention au cas particulier...)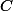 , la lettre i sert déjà...]
, la lettre i sert déjà...]. Calcule ensuite de deux manières différentes
.
\pi}{2n}\right)=\frac{1}{2^{n-1}})
\pi}{n}\right)) est nul lorsque n est impair, vu qu'il contient
est nul lorsque n est impair, vu qu'il contient =0)
