[Défi] Polynômes cyclotomiques
58 messages
- Page 2 sur 3 - 1, 2, 3
Re !
J'ai finalement réussi la question 6. Ensuite j'ai réussi la 8 grâce à la 7 par une récurrence.
Par contre pour la 7 comment dois-je faire ? Je n'arrive pas trop trop a voir. D'après moi je dois transformer les écritures et arriver à ce que je veut, mais mon problème c'est le x^k qui apparaît.
Merci beaucoup !
J'ai finalement réussi la question 6. Ensuite j'ai réussi la 8 grâce à la 7 par une récurrence.
Par contre pour la 7 comment dois-je faire ? Je n'arrive pas trop trop a voir. D'après moi je dois transformer les écritures et arriver à ce que je veut, mais mon problème c'est le x^k qui apparaît.
Merci beaucoup !
La 7) est une application de la 6) :
Tu l'utilise pour évaluer psi_(pn)(x) où deux cas sont à étudier pour l'ensembles des diviseurs de np selon que n est ou pas multiple de p.
Ensuite, dans chaque cas, tu utilise la 6) pour évaluer psi_n(x^p) ou psi_n(x^p)/psi_n(x).
Tu trouve bien que c'est la même chose (faire attention à bien repérer quel sont les mu(d) qui sont nuls et donc ne servent à rien...)
Tu l'utilise pour évaluer psi_(pn)(x) où deux cas sont à étudier pour l'ensembles des diviseurs de np selon que n est ou pas multiple de p.
Ensuite, dans chaque cas, tu utilise la 6) pour évaluer psi_n(x^p) ou psi_n(x^p)/psi_n(x).
Tu trouve bien que c'est la même chose (faire attention à bien repérer quel sont les mu(d) qui sont nuls et donc ne servent à rien...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Quand p divise n pas de problèmes. Par contre, quand p ne divise pas n alors j'ai des soucis.
Je dois montrer que
^{\mu(d)}}{ \bigprod_{d|n}(x^{\frac{n}{d}}-1)^{\mu(d)}}=\bigprod_{d|pn}(x^{\frac{pn}{d}}-1)^{\mu(d)})
et je n'y arrive plus, je ne vois pas vraiment quoi faire ensuite .
Sinon, question 9 l'énoncé est-il bon ?
Enfin, je viens de remarquer que la 12 est un corollaire immédiat de la 11.
Merci à vous !
Je dois montrer que
et je n'y arrive plus, je ne vois pas vraiment quoi faire ensuite .
Sinon, question 9 l'énoncé est-il bon ?
Enfin, je viens de remarquer que la 12 est un corollaire immédiat de la 11.
Merci à vous !
Pour la 9), l'énoncé est trés ambigü et l'interprétation que risque d'en faire un lycéen fait que le résultat est faux :
Par exemple, si p=2 alors il est clair que, pour tout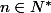 et tout
et tout  on a
on a  donc
donc
^2\times 1\ [2]) que n soit divisible par p=2 ou pas : le résultat demandé est donc faux.
que n soit divisible par p=2 ou pas : le résultat demandé est donc faux.
Pour que le résultat demandé soit juste, il ne faut pas interpréter la relation^2\times f(x)\ [p]) comme signifiant "
comme signifiant "^2\times f(x)\ [p]) " mais comme signifiant que les polynômes formels
" mais comme signifiant que les polynômes formels 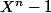 et
et ^2\times f(X)) sont égaux modulo p.
sont égaux modulo p.
Bon, évidement, la question qui tue, c'est "c'est quoi un polynôme 'formel' ? et ça veut dire quoi que deux polynômes 'formels' sont égaux ?"
Un polynôme formel sur un corps K (ou sur un anneau) c'est une expression de la forme=a_0+a_1X+a_2X^2+...+a_dX^d) où
où  sont des éléments de K mais où X n'est pas un élément de quelque chose : c'est une 'variable formelle'. En particulier, un polynôme formel n'est pas une fonction d'un ensemble dans un autre ce qui signifie en particulier que, pour que les polynômes formels P et Q soit égaux, il ne suffit pas de vérifier que P(x)=Q(x) pour tout élément x de K.
sont des éléments de K mais où X n'est pas un élément de quelque chose : c'est une 'variable formelle'. En particulier, un polynôme formel n'est pas une fonction d'un ensemble dans un autre ce qui signifie en particulier que, pour que les polynômes formels P et Q soit égaux, il ne suffit pas de vérifier que P(x)=Q(x) pour tout élément x de K.
Par définition, deux polynômes formel sont égaux lorsqu'ils ont les même coefficients.
Exemple : Si on considère les polynômes P(X)=X et P(X)=X² à coeff dans Z/2Z (i.e. modulo 2) alors les fontions polynômes P et Q sont égales (c'est à dire que, pour tout x de Z/2Z on a bien x²=x) mais les polynômes formels P et Q ne sont pas égaux !
Evidement, si deux polynômes formels sont égaux, alors les fonctions polynômes correspondantes sont égales (si deux polynômes ont les même coeffs, alors il donne le même résultat lorsque l'on remplace x par un elément de K) mais la réciproque n'est vrai que si le corps K et infini.
Comme au lycée on ne manipule que des polynômes vu comme fonction de R dans R ou de C dans C et que R et C sont infinis, il n'y a pas de raison de faire de différence entre les deux notions (fonctions polynôme et polynômes formels). Il en va tout autrement lorsque l'on manipule des polynômes à coeff dans Z/pZ qui lui est fini : deux fonctions polynômes peuvent tout à fait être égales sans que pour autant leurs coefficients soient égaux...
Bon, en résumé, la question 9) est juste si on considère que l'on parle de polynomes formels. Sauf que, parmi ce que tu sait concernant les polynômes, je pense que ça risque d'être difficile de savoir quels résultats restent vrais pour les polynômes formels et lesquels deviennent faux (en plus, ça risque surtout de t'embrouiller complètement...)
Par exemple, si p=2 alors il est clair que, pour tout
Pour que le résultat demandé soit juste, il ne faut pas interpréter la relation
Bon, évidement, la question qui tue, c'est "c'est quoi un polynôme 'formel' ? et ça veut dire quoi que deux polynômes 'formels' sont égaux ?"
Un polynôme formel sur un corps K (ou sur un anneau) c'est une expression de la forme
Par définition, deux polynômes formel sont égaux lorsqu'ils ont les même coefficients.
Exemple : Si on considère les polynômes P(X)=X et P(X)=X² à coeff dans Z/2Z (i.e. modulo 2) alors les fontions polynômes P et Q sont égales (c'est à dire que, pour tout x de Z/2Z on a bien x²=x) mais les polynômes formels P et Q ne sont pas égaux !
Evidement, si deux polynômes formels sont égaux, alors les fonctions polynômes correspondantes sont égales (si deux polynômes ont les même coeffs, alors il donne le même résultat lorsque l'on remplace x par un elément de K) mais la réciproque n'est vrai que si le corps K et infini.
Comme au lycée on ne manipule que des polynômes vu comme fonction de R dans R ou de C dans C et que R et C sont infinis, il n'y a pas de raison de faire de différence entre les deux notions (fonctions polynôme et polynômes formels). Il en va tout autrement lorsque l'on manipule des polynômes à coeff dans Z/pZ qui lui est fini : deux fonctions polynômes peuvent tout à fait être égales sans que pour autant leurs coefficients soient égaux...
Bon, en résumé, la question 9) est juste si on considère que l'on parle de polynomes formels. Sauf que, parmi ce que tu sait concernant les polynômes, je pense que ça risque d'être difficile de savoir quels résultats restent vrais pour les polynômes formels et lesquels deviennent faux (en plus, ça risque surtout de t'embrouiller complètement...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
:id: Ok, ... quelle rapidité !!
Alors il n'y a pas moyen d'éludé la question ( mais je suppose qu'on en a besoin ! ) ou que que tu me passe une répopnse histoire que je te dise ce que je comprend/ ne comprend pas ?
En tout cas merci pour ce post très instructifs. En plus j'ai toujours pas fait d'algèbre des Polynômes donc j'y connais que dalle ..
Alors il n'y a pas moyen d'éludé la question ( mais je suppose qu'on en a besoin ! ) ou que que tu me passe une répopnse histoire que je te dise ce que je comprend/ ne comprend pas ?
En tout cas merci pour ce post très instructifs. En plus j'ai toujours pas fait d'algèbre des Polynômes donc j'y connais que dalle ..
Si tu veut chercher la 9), ce que tu as besoin de savoir :
1) On peut évidement ajouter, soustraire, multiplier des polynômes formels (et le résultat est un polynôme formel). Par contre, évidement, on ne peut pas toujour diviser (il y a une notion de division euclidienne comme pour les entiers)
2) On peut parfaitement définir la dérivée d'un polynôme formel :
Si=a_0+a_1X+a_2X^2+\cdots a_dX^d) on définit
on définit =a_1+2a_2X+3a_3X^2+\cdots da_dX^{d-1}) où les entiers
où les entiers  sont à interpréter comme des éléments de K (
sont à interpréter comme des éléments de K (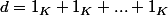 d fois où
d fois où  désigne l'élément neutre de la multiplication dans K.
désigne l'élément neutre de la multiplication dans K.
Exemple: dans Z/5Z, si=1+3X^2+4X^3+X^5) alors
alors =6X+12X^2+5X^4=X+2X^2) (noter que
(noter que \not=d^o(P)-1) ).
).
Faire attention que cette définition n'a strictement rien à voir avec les limites : on ne peut pas définir la notion de limite sur Z/5Z !!!
3) Les formules usuelles de dérivation sont encore valable : (P+Q)'=P'+Q' , (aP)'=a(P') ; (PxQ)'=P'Q+PQ' [Tu peut les démontrer si tu veux : attention seulement à bien utiliser la nouvelle définition et surtout pas des propriétés connues des fonction polynômes]
4) On peut mettre (X-a) en facteur dans un polynôme formel P ssi P(a)=0 (ici, lorsque l'on écrit P(a), on parle bien entendu de la fonction polynôme associée à P : certains auteurs écrive) pour bien faire la différence, mais c'est un peu chiant, donc souvent on fait un "abus de langage" en écrivant directement P(a))
pour bien faire la différence, mais c'est un peu chiant, donc souvent on fait un "abus de langage" en écrivant directement P(a))
[Tu peut démontrer ce résultat, ce n'est pas trop compliqué : attention de nouveau à n'utiliser aucun résultats concernant les fonctions polynômes !!!]
4) On peut mettre (X-a)² en facteur dans un polynôme formel P ssi P(a)=P'(a)=0. [Pas trop compliqué à démontrer]
5) Attention par contre au fait que ça ne marche pas "plus loin" : si on peut mettre (X-a)^3 en facteur dans P(X) alors P(a)=P'(a)=P"(a)=0, mais la réciproque est fausse : par exemple dans Z/2Z, si P(X)=X^2 alors P'(X)=2X=0 et P"(X)=0 donc P(0)=P'(0)=P"(0) mais on ne peut pas mettre (X-0)^3 en facteur dans P(X)=X^2 !!! (en fait la réciproque est vrai uniquement lorsque dans le corps K sur lequel on travaille)
dans le corps K sur lequel on travaille)
1) On peut évidement ajouter, soustraire, multiplier des polynômes formels (et le résultat est un polynôme formel). Par contre, évidement, on ne peut pas toujour diviser (il y a une notion de division euclidienne comme pour les entiers)
2) On peut parfaitement définir la dérivée d'un polynôme formel :
Si
Exemple: dans Z/5Z, si
Faire attention que cette définition n'a strictement rien à voir avec les limites : on ne peut pas définir la notion de limite sur Z/5Z !!!
3) Les formules usuelles de dérivation sont encore valable : (P+Q)'=P'+Q' , (aP)'=a(P') ; (PxQ)'=P'Q+PQ' [Tu peut les démontrer si tu veux : attention seulement à bien utiliser la nouvelle définition et surtout pas des propriétés connues des fonction polynômes]
4) On peut mettre (X-a) en facteur dans un polynôme formel P ssi P(a)=0 (ici, lorsque l'on écrit P(a), on parle bien entendu de la fonction polynôme associée à P : certains auteurs écrive
[Tu peut démontrer ce résultat, ce n'est pas trop compliqué : attention de nouveau à n'utiliser aucun résultats concernant les fonctions polynômes !!!]
4) On peut mettre (X-a)² en facteur dans un polynôme formel P ssi P(a)=P'(a)=0. [Pas trop compliqué à démontrer]
5) Attention par contre au fait que ça ne marche pas "plus loin" : si on peut mettre (X-a)^3 en facteur dans P(X) alors P(a)=P'(a)=P"(a)=0, mais la réciproque est fausse : par exemple dans Z/2Z, si P(X)=X^2 alors P'(X)=2X=0 et P"(X)=0 donc P(0)=P'(0)=P"(0) mais on ne peut pas mettre (X-0)^3 en facteur dans P(X)=X^2 !!! (en fait la réciproque est vrai uniquement lorsque
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ou la .. merci pour tout ça :id:
Donc, en gros, il faut montrer que si F(k)=F'(k)=0 [p] avec F(x)=x^n-1 alors on a p divise n .. je vois vraiment pas comment m'en sortir :doh: mais alors vraiment pas . Comment commencer au moins ?
Merci ! :we:
( Désolé de ne pas y arriver même avec tout ca :marteau: )
Donc, en gros, il faut montrer que si F(k)=F'(k)=0 [p] avec F(x)=x^n-1 alors on a p divise n .. je vois vraiment pas comment m'en sortir :doh: mais alors vraiment pas . Comment commencer au moins ?
Merci ! :we:
( Désolé de ne pas y arriver même avec tout ca :marteau: )
J'en profite, pour demander des indications :
10- Quelqun peut-il proposer une réécriture de cette question ? Il semble y avoir une erreur ...
11- Es-ce que je pourrais avoir des pistes s'il vous plait ? Je vois pas trop comment faire. A part que p divise Phi_n(x) ==> x^n=1[p] mais c'est tout .
Je vous remercie !!
10- Quelqun peut-il proposer une réécriture de cette question ? Il semble y avoir une erreur ...
11- Es-ce que je pourrais avoir des pistes s'il vous plait ? Je vois pas trop comment faire. A part que p divise Phi_n(x) ==> x^n=1[p] mais c'est tout .
Je vous remercie !!
Pour la 9), si tu as montré les propriétés des polynômes formels mentionnés dans le post #29, c'est trés simple :
L'hypothése dit qu'il existe un tel que
tel que^2) divise
divise =X^n-1) ce qui signifie que
ce qui signifie que =P'(a)=0) , c'est à dire que
, c'est à dire que  et que
et que  .
.
Or donc
donc  , ce qui signifie que p divise n.
, ce qui signifie que p divise n.
Pour la 10), c'est une déduction assez simple de la 9) et une "étape" pour montrer une partie de la 11), sauf que c'est un peu n'importe quoi...
Indic : Le polynôme\times\Phi_d(X)) divise
divise 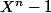 .
.
Pour la 11), déjà, prend à la place de
à la place de  (je comprend pas pourquoi il change certaines lettres de questions en question...).
(je comprend pas pourquoi il change certaines lettres de questions en question...).
Indic : Si divise
divise ) alors dans
alors dans  , on a
, on a =0) mais, comme le polynôme
mais, comme le polynôme 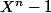 est divisible par
est divisible par ) , on a aussi
, on a aussi  (toujours dans
(toujours dans  ) ce qui signifie évidement que
) ce qui signifie évidement que 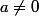 et que, si on note
et que, si on note  l'ordre multiplicatif de
l'ordre multiplicatif de  dans K, alors
dans K, alors  divise
divise  .
.
D'un autre coté, le petit théorème de fermat nous dit aussi que divise
divise  .
.
Là, deux cas se présentent :
Soit d=n et on a ....
Soit d est distinct de n et on a ...
L'hypothése dit qu'il existe un
Or
Pour la 10), c'est une déduction assez simple de la 9) et une "étape" pour montrer une partie de la 11), sauf que c'est un peu n'importe quoi...
10) Soitest un entier naturel,
un diviseur de
distinct de
,
un entier relatif et
un nombre premier tel que
divise à la fois
et
.
Montrer quedivise
Indic : Le polynôme
Pour la 11), déjà, prend
Indic : Si
D'un autre coté, le petit théorème de fermat nous dit aussi que
Là, deux cas se présentent :
Soit d=n et on a ....
Soit d est distinct de n et on a ...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut !
Pour la 13 j'ai réussi avec ta (très astucieuse ! ) indication ! D'ailleurs je l'aurais certainement pas trouvé tout seul !
Pour la 14, je présume que c'est une appli du 13, mais là aussi je n'y arrive pas, je trouve pas de méthode
Comment faut-il procéder ?
Merci :id:
PS: Pour la dernière application, pour résoudre dans Z=y^5-1) Comment continuer ? :happy3:
Comment continuer ? :happy3:
Pour la 13 j'ai réussi avec ta (très astucieuse ! ) indication ! D'ailleurs je l'aurais certainement pas trouvé tout seul !
Pour la 14, je présume que c'est une appli du 13, mais là aussi je n'y arrive pas, je trouve pas de méthode
Comment faut-il procéder ?
Merci :id:
PS: Pour la dernière application, pour résoudre dans Z
Pour la 14), le seul truc que je vois utilise un peu tout ce qui a été fait...
- Montrer à l'aide de 8) que) divise
divise ) et en déduire que l'on peut sans perte de généralité supposer
et en déduire que l'on peut sans perte de généralité supposer 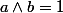 .
.
- Vu que\wedge\Phi_b(x)\not=1) , il existe un nombre premier
, il existe un nombre premier  qui divise
qui divise ) et
et ) .
.
Montrer à l'aide de 13) que divise
divise ) puis en utilisant 10) que, quitte à échanger
puis en utilisant 10) que, quitte à échanger  et
et  , on a
, on a 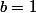 et, si
et, si 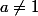 alors
alors  divise
divise  .
.
- Si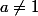 , écrire
, écrire  où
où  ne divise pas
ne divise pas 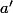 et
et  .
.
Montrer que, si on pose , alors
, alors  divise
divise) ainsi que
ainsi que ) .
.
En déduire à l'aide de 13) que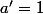 .
.
A noter une erreur dans cette question 14) : On obtient que avec
avec 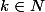 en ayant éventuellement échangé a et b donc le résultat demandé est (encore !!!) faux : on a seulement
en ayant éventuellement échangé a et b donc le résultat demandé est (encore !!!) faux : on a seulement  avec
avec  ce qui n'est pas surprenant vu que a et b jouent le même rôle !!!
ce qui n'est pas surprenant vu que a et b jouent le même rôle !!!
Pour les différentes applications, comme c'est moins du "super classique" que le début, il faut que je regarde (et j'ai pas trop le temps ce matin...)
- Montrer à l'aide de 8) que
- Vu que
Montrer à l'aide de 13) que
- Si
Montrer que, si on pose
En déduire à l'aide de 13) que
A noter une erreur dans cette question 14) : On obtient que
Pour les différentes applications, comme c'est moins du "super classique" que le début, il faut que je regarde (et j'ai pas trop le temps ce matin...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Alors, j'ai lu tout ce que tu as marqué, et j'arrive pas a montrer que on peut supposer pgcd(a,b)=1 ? :doh:
Je ne comprends pas comment faire quand tu dit :
Comment montrer que p divise le premier polynome cyclotomique, et en déduire que a'=1 ?
Merci !
Je ne comprends pas comment faire quand tu dit :
Ben a écrit:- Si, écrire
où p ne divise pas a' et
.
Montrer que, si on pose, alors p divise
ainsi que
.
En déduire à l'aide de 13) que a'=1.
Comment montrer que p divise le premier polynome cyclotomique, et en déduire que a'=1 ?
Merci !
En écrivant  et en faisant une réccurence sur k, on montre à l'aide de la question 8) que
et en faisant une réccurence sur k, on montre à l'aide de la question 8) que ) divise
divise ) (on doit aussi pouvoir le faire directement à l'aide de la question 6)...)
(on doit aussi pouvoir le faire directement à l'aide de la question 6)...)
Dans la question 14), on pose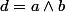 : on a donc
: on a donc  et
et  où
où 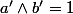 .
.
La remarque ci dessus montre que) divise
divise ) et que
et que ) divise
divise ) . L'hypothèse
. L'hypothèse \wedge\Phi_{b}(x)\not=1) implique donc que
implique donc que \wedge\Phi_{b'}(x^d)\not=1) .
.
Comme il suffit de montrer le résultat est vrai pour le triplet
il suffit de montrer le résultat est vrai pour le triplet ) et cela prouvera qu'il est vrai pour le triplet (a,b,x).
et cela prouvera qu'il est vrai pour le triplet (a,b,x).
Cela revient bien à dire que l'on peut, sans perte de généralité supposer que a et b sont premiers entre eux.
A la fin de la preuve, on sait que b=1 donc, si a=1 alors et le résultat demandé est vrai.
et le résultat demandé est vrai.
Si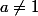 on sait que dans ce cas p divise a et on peut écrire
on sait que dans ce cas p divise a et on peut écrire  où
où 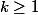 et a' non divisible par p (on factorise la plus grande puissance possible de p dans a).
et a' non divisible par p (on factorise la plus grande puissance possible de p dans a).
On sait que p divise=\Phi_{p^ka'}(x)) qui lui même divise
qui lui même divise ) [question 8)].
[question 8)].
On sait aussi que p divise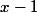 qui lui même divise tout
qui lui même divise tout  donc en particulier
donc en particulier )
Le nombre premier p divise donc simultanément) et
et ) ce qui, si 1<a' impliquerait que p divise a' [Question 10)].
ce qui, si 1<a' impliquerait que p divise a' [Question 10)].
Comme on sait que p ne divise pas a', cela signifie qu'en fait a'=1.
Dans la question 14), on pose
La remarque ci dessus montre que
Comme
Cela revient bien à dire que l'on peut, sans perte de généralité supposer que a et b sont premiers entre eux.
A la fin de la preuve, on sait que b=1 donc, si a=1 alors
Si
On sait que p divise
On sait aussi que p divise
Le nombre premier p divise donc simultanément
Comme on sait que p ne divise pas a', cela signifie qu'en fait a'=1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci beaucoup !! C'est vraiment plus clair maintenant :we:
Maintenant .. les applications,
Pour le théorème de Dirichlet, je n'arrive pas a trouver comment montrer l'infinité de ces nombres , comment procéder ?
(Je pensais faire une preuve comme Euclide par l'absurde, mais j'arrive pas à la concrétiser ...)
Merci encore :zen:
Maintenant .. les applications,
Pour le théorème de Dirichlet, je n'arrive pas a trouver comment montrer l'infinité de ces nombres , comment procéder ?
(Je pensais faire une preuve comme Euclide par l'absurde, mais j'arrive pas à la concrétiser ...)
Merci encore :zen:
58 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
