Défi 2.8
Olympiades mathématiques, énigmes et défis
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 11 Juin 2007, 19:08
par fahr451 » 11 Juin 2007, 19:08
un exercice taupinal (j 'espère que personne n'a rien contre, moi j'aime bien ,la taupe c'est un peu mon eldorado et c'est la période des oraux )
donner un équivalent en 0+
de f(x) = intégrale de 0 à +infini t/(1+t^2) exp(-tx) dt
une ame charitable pour l'écrire de façon lisible
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 11 Juin 2007, 19:37
par Imod » 11 Juin 2007, 19:37
Donner un équivalent en 0+
de
 = \int_0^{+\infty}\frac{t}{1+t^2}.e^{-tx}dt})
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 11 Juin 2007, 19:40
par Alpha » 11 Juin 2007, 19:40
Le TEX n'est pas ton Eldorado en tout cas, fahr :ptdr:
:lol4:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 11 Juin 2007, 19:44
par fahr451 » 11 Juin 2007, 19:44
merci bien imod
alpha c 'est un tit exo de l X (un pas dur ... :id: ;ah voila je suis mesquin aussi)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juin 2007, 21:09
par yos » 11 Juin 2007, 21:09
Je trouve -ln x mais j'ai la flemme de rédiger. Alors déjà : est-ce que c'est ça?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 11 Juin 2007, 21:11
par fahr451 » 11 Juin 2007, 21:11
oui
tu prépares l'oral yos ? :we:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juin 2007, 21:14
par yos » 11 Juin 2007, 21:14
fahr451 a écrit:oui
tu prépares l'oral yos ? :we:
Oui mais comme je suis né en 93, je n'ai pas l'autorisation de présenter l'X, alors je fais ça pour le fun.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 11 Juin 2007, 21:21
par fahr451 » 11 Juin 2007, 21:21
quatre ans après la grande exposition universelle à paris quelle chance!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Juin 2007, 21:26
par yos » 11 Juin 2007, 21:26
Non c'est l'année de la Terreur.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 12 Juin 2007, 13:12
par yos » 12 Juin 2007, 13:12
Quelques détails pour ce défi 2.8.
Pour x>0,
=\int_0^{+\infty}\frac{-t^2}{1+t^2}e^{-tx}dt)
(égalité due à la cvu de cette intégrale sur
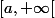
pour tout a>0).
D'où
=\int_0^{+\infty}\frac{1}{1+t^2}e^{-tx}dt-\int_0^{+\infty}e^{-tx}dt=K-\frac{1}{x}\sim -\frac{1}{x})
.
Le réel K étant au plus égal à

, soit
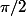
.
Après on intègre les deux membres, ce qui est licite dés que l'une des fonctions garde un signe constant au voisinage de 0.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 12 Juin 2007, 13:24
par fahr451 » 12 Juin 2007, 13:24
ah j'avais pas fait ça
u = tx puis l'intégrale entre 1 et +inf est bornée
reste u/(x^2+u^2) exp (-u) du entre 0 et 1 que j'ai froidement remplacé par celle de u/(x^2 +u^2)
la différence restant bornée car l 1 -exp(-u) l = < u sur [0,1]
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 12 Juin 2007, 13:41
par yos » 12 Juin 2007, 13:41
C'est bien aussi. Allez je lance un 2.9.
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 12 Juin 2007, 17:21
par Alpha » 12 Juin 2007, 17:21
Tu es né en 93, yos??? :doh:
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 12 Juin 2007, 20:24
par yos » 12 Juin 2007, 20:24
Alpha a écrit:Tu es né en 93, yos???
Quoi? c'est pas le site second life ici?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 12 Juin 2007, 20:57
par fahr451 » 12 Juin 2007, 20:57
tiens alpha je m 'en vas te dire un s'cret
yos trafique son âge histoire de faire le beau
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
