et ça me permet de dire que An est non nul ? ( désolé je vois pas ... )
Après dans la suite de l'énoncé, sur l'irrationalité de pi je suis boqué sur les deux et sur ln(2) je coince à la deuxième.
PS: J'ai trouvé pourquoi An n'était pas nul. PAr contre pour la 2 de l'irrationnalité de pi comment doit-on faire ? Merci !
[Défi] Irrationalité de Pi et ln 2, méthode intégrale
24 messages
- Page 2 sur 2 - 1, 2
Pour l'irrationalité de ln(2), on prend =\frac{1}{1+x}) .
.
1) Montre que, pour tout\,dx=\frac{a_n}{d_n}+(-1)^n\ln(2)) où
où 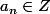 et
et 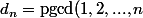) puis déduit en que, pour tout
puis déduit en que, pour tout 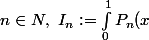f(x)\,dx=\frac{b_n}{d_n}+c_n\ln(2)) où
où 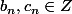 et
et =\frac{1}{n!}\frac{\partial^n(x(1-x))^n}{\partial x^n})
2) Montre que, pour tout}(x)=(-1)^n\frac{n!}{(1+x)^{n+1}}) et déduit en que
et déduit en que 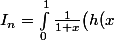\big)^ndx) où
où =\frac{x(1-x)}{1+x}) puis, en étudiant
puis, en étudiant ) sur [0,1], déduit en que
sur [0,1], déduit en que 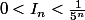
3) On déduit du 1) et du 2) que, pour tout<\frac{d_n}{5^n}) .
.
Si ln(2) était un quotient on aurait=\frac{p}{q}) or, dés que
or, dés que 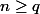 , l'entier
, l'entier  divise
divise 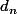 (par définition de
(par définition de 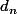 ) donc
) donc =d_n\frac{p}{q}) est entier et donc (toujours lorsque
est entier et donc (toujours lorsque 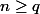 ),
), ) est un entier strictement compris entre 0 et
est un entier strictement compris entre 0 et 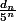 .
.
Si on montre que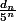 tend vers 0, on tombe donc sur une belle contradiction.
tend vers 0, on tombe donc sur une belle contradiction.
Sauf que, si on regarde les différentes puissances de nombres premiers qui apparaissent dans les entiers 1,2,3,...,n, on voit que}{\ln(p)}\Big)) où la somme se fait sur les nombres premiers
où la somme se fait sur les nombres premiers 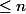 et
et ) la partie entière du réel
la partie entière du réel  .
.
On en déduit que=\bigsum_{p\leq n}E\Big(\frac{\ln(n)}{\ln(p)}\Big)\ln(p) \leq \bigsum_{p\leq n}\frac{\ln(n)}{\ln(p)}\ln(p)=\pi(n)\ \ln(n)) où
où ) désigne le nombre de nombre premiers
désigne le nombre de nombre premiers 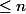 .
.
Or, comme tout lycéen doit bien évidement le savoir (!!!!!!),) est équivalent à
est équivalent à }) lorsque
lorsque 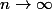 donc
donc ) est équivalent à
est équivalent à  et cela prouve que
et cela prouve que =\ln(d_n)-n\ln(5)) tend vers
tend vers  , c'est à dire que
, c'est à dire que 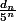 tend vers 0.
tend vers 0.
C'est effectivement parfaitement accéssible au Lycée !!!
1) Montre que, pour tout
2) Montre que, pour tout
3) On déduit du 1) et du 2) que, pour tout
Si ln(2) était un quotient on aurait
Si on montre que
Sauf que, si on regarde les différentes puissances de nombres premiers qui apparaissent dans les entiers 1,2,3,...,n, on voit que
On en déduit que
Or, comme tout lycéen doit bien évidement le savoir (!!!!!!),
C'est effectivement parfaitement accéssible au Lycée !!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
24 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
