[Défi] Racines n-ième
Olympiades mathématiques, énigmes et défis

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mai 2010, 14:54
par Ben314 » 12 Mai 2010, 14:54
Aux erreurs de calculs possibles prés, c'est bien ça.
Bon, évidement, il faudrait arriver à exprimer ça différement : P(n+1) est évidement un réel...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Mai 2010, 15:23
par benekire2 » 12 Mai 2010, 15:23
mon calcul est faux ?
J'obtiens donc
=1-(i \sqrt{3}e^{\frac{i4\pi}{3}})^{3n+1}(\frac{2}{3}+ \frac {1}{3} e^{\frac{2i \pi}{3}})-(i \sqrt{3 }e^{\frac{i 2\pi}{3}})^{3n+1}(\frac{2}{3}+\frac{1}{3}e^{\frac{4i \pi}{3}}))
Après faut même que je change le 2/3+1/3e^i .. ou pas ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mai 2010, 15:47
par Ben314 » 12 Mai 2010, 15:47
Perso, je pense que le "joli" résultat final, ben faudrait qu'il y ait plus de complexes dedans, donc oui, tu évalue tout et même, tu fait trois cas selon le reste de la division par 3 de n.
Ca te permet en plus de voir si tu t'es gourré ou pas car la forme qu tu avait plus haut de P(3n+1) montre que, non seulement ç'est un réel (donc pas de 'i') mais même que c'est un entier...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Mai 2010, 16:42
par benekire2 » 12 Mai 2010, 16:42
Ca commence a me gonfler, :zen: trois pages de calculs et je tombe sur P(3n+1)=1 .... puisque 1+e^i2pi/3+e^i4pi/3=0 ... j'ai dû faire une erreur quelque part !
Si tu sais où elle est dit moi , sinon je cherche :doh:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mai 2010, 17:16
par Ben314 » 12 Mai 2010, 17:16
Bon, en testant avec Mapple, la formule du post #122 donne bien 1 en permanence (donc elle est fausse...)
celle du post #119 aussi est fausse (mais celle là, elle donne pas 1 en permanence... :doh: )
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Mai 2010, 17:49
par benekire2 » 12 Mai 2010, 17:49
c'est donc une double faute. Effectivement en refaisant les calculs j'arrive à :
=1-\frac{(i\sqrt{3})^{3n+1}((-1)^n e^{\frac{\pi}{3}}(2+e^{\frac{i4\pi}{3}})+e^{\frac{i\pi}{3}}(2+e^{\frac{2\pi}{3}}))}{3})
si jamais c'est ça ... on continue comment ? Encore développer ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 12 Mai 2010, 18:20
par Zweig » 12 Mai 2010, 18:20
Je n'ai pas vérifié tous tes calculs (j'étais parti différemment au début) mais (pour que tu puisses vérifier) on doit trouver n = 4.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Mai 2010, 18:40
par benekire2 » 12 Mai 2010, 18:40
Zweig a écrit:Je n'ai pas vérifié tous tes calculs (j'étais parti différemment au début) mais (pour que tu puisses vérifier) on doit trouver n = 4.
Merci beaucoup !
Donc, ma formule est archi fausse !
Et a mon avis l'erreur doit remonter d'il y a ... longtemps longtemps ....
Est-on tous d'accord que :
\ =-( 2\Bigsum_{\matrix{j=0\cr j\equ0\ [3]}}^{3n+1}(-1)^{3n+1-j}C_{3n+1}^j +\Bigsum_{\matrix{j=0\cr j\equ1\ [3]}}^{3n+1}[(-1)^{3n+1-j}C_{3n+1}^j]-1))
Si quelqu'un peut vérifier avec mapple .. merci :we:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Mai 2010, 18:46
par Ben314 » 12 Mai 2010, 18:46
Jusque là, ça semble correct.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Mai 2010, 18:50
par benekire2 » 12 Mai 2010, 18:50
^{3n+1-j}C_{3n+1}^j=\frac{2}{3}\Bigsum_{t=1}^{2}(\omega ^t-1)^{3n+1})
^{3n+1-j}C_{3n+1}^j=\frac{1}{3}\Bigsum_{t=0}^{2}\omega ^{-t}(\omega ^t -1)^{3n+1})
On est d'accord là dessus ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 12 Mai 2010, 19:08
par Zweig » 12 Mai 2010, 19:08
Salut,
Une autre manière de faire est de partir de
 = P(x)-1)
et d'appliquer le théorème de Lagrange dessus.
On trouve
 = \displaystyle \sum^{3n}_{i=0}(-1)^{3n-i}C^{i}_{3n+1}Q(i))
On utilise la formule de multi-section au polynôme
 = \displaystyle \sum^{3n+1}_{i=0}C^{i}_{3n+1}x^i = (1+x)^{3n+1})
Sauf erreur, on trouve :
 = (-1)^{3n}\displaystyle \sum^{5}_{i=0}f(\omega_i)(1-\omega_i^{-2} - \omega_i^{-3} - \omega_i^{-5}))
avec
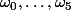
les 6 racines de l'unité.
En bidouillant un peu on arrive à :
 = 2\cdot (-1)^{3n}\cdot 3^{\frac{3n}{2}}\cdot \cos\,\left(\frac{n\pi}{2} + \frac{\pi}{3}\right))
Or
 = 730 - 1 = 3^6)
, d'où
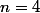
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 12 Mai 2010, 20:57
par benekire2 » 12 Mai 2010, 20:57
a mon avis, avec "notre" méthode on devait sensiblement retomber sur la même chose, c'est juste que j'ai merder à un endroit ...
Mais sinon, c'est le même principe en fait !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
