Défi Enigme

par **_-Gaara-_** » 14 Juil 2008, 16:35

Salut,

alors voilà un petit problème pour toi cher lecteur =)

Tu as un nombre au hasard entre 0et 1. A ce nombre, tu ajoute un autre nombre aléatoirement choisi entre 0 et 1. Tu itères le processus jusqu'à la somme dépasse 1.De combien de nombres, en moyenne, auras tu besoin ?

Je poste la solution dans 1 semaine si personne ne la trouve.

Bon courage !!!!!!

par **guigui51250** » 14 Juil 2008, 17:57

_-Gaara-_ a écrit:Salut,

alors voilà un petit problème pour toi cher lecteur =)

Je poste la solution dans 1 semaine si personne ne la trouve.

Bon courage !!!!!!

euh bah moi je crois que je vais sagement attendre une semaine au lieu de dire des conneries ^^ et je ne peux même pas donner une idée parce que j'en sais rien du tout ^^

par **le_fabien** » 14 Juil 2008, 18:26

Bonsoir,
cela me fait penser à la loi uniforme continue sur [0;1].

par **le_fabien** » 14 Juil 2008, 18:43

Son espérance étant égale à

je pense que le nombre de processus sera de deux. :happy:

par **ThSQ** » 14 Juil 2008, 20:09

Heu ....

"" a écrit:e

par **_-Gaara-_** » 14 Juil 2008, 20:31

ThSQ :

pourquoi?

LEFAB11 : c'est bien plus complicated :++: :++:

par **reday** » 14 Juil 2008, 20:55

bonsoir à tous

ce nombre qu'on cherche ne tend pas t'il vers plus l'infini

par **ThSQ** » 14 Juil 2008, 21:03

_-Gaara-_ a écrit:Why

Somme de probas conditionnels qui se visualisent très bien en coupant des carrés, des cubes, des hypercubes ...

par **Clembou** » 14 Juil 2008, 22:29

_-Gaara-_ a écrit:Tu as un nombre au hasard entre 0et 1. A ce nombre, tu ajoute un autre nombre aléatoirement choisi entre 0 et 1. Tu itères le processus jusqu'à la somme dépasse 1.De combien de nombres, en moyenne, auras tu besoin ?

J'ai besoin de quelques précisions :

On prend donc un nombre au hasard entre 0 et 1.
On ajoute un autre nombre au hasard entre 0 et 1.
Et on le fait jusqu'à ce que la somme soit

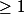
ou

?

par **_-Gaara-_** » 15 Juil 2008, 05:01

Clembou : >1

ThSQ : lol ce que tu m'as donné n'a pas le statu de démonstration mathématique :we:

reday : étonnamment non, c'est ça qui fait la beauté du truc

par **le_fabien** » 15 Juil 2008, 07:36

_-Gaara-_ a écrit:ThSQ :

LEFAB11 : c'est bien plus complicated :++: :++:

Bof...j'aime bien voir les choses simplement. :lol:

Je trouvais que c'était une bonne idée.

par **ThSQ** » 15 Juil 2008, 08:04

_-Gaara-_ a écrit:le statu

Le statu quo sans doute.

par **_-Gaara-_** » 15 Juil 2008, 08:25

ThSQ a écrit:Le statu quo sans doute.

Je m'attendais à plus drôle, en vain.

par **Flodelarab** » 15 Juil 2008, 14:15

SexyBoy a écrit:Mais il y a quand meme un autre probleme qui se pose: si jamais on tombe sur un cas qui ne dépasse jamais 1

Moi je suis mauvais mais je sais que si je lance un dé a 6 faces non pipé, j'ai une chance sur 6 de faire 6. Et pourtant, je peux lancer 10Mards de fois un dé sans jamais faire 6.
Je ne vois pas en quoi ton objection fait avancer le problème.

par **Imod** » 15 Juil 2008, 15:37

Si je dis qu'il faut en moyenne

nombres pour dépasser 1 ça suffit ?

Imod

par **_-Gaara-_** » 15 Juil 2008, 15:45

Imod a écrit:Si je dis qu'il faut en moyenne nombres pour dépasser 1 ça suffit ?

Imod

Il faut la démonstration , Imod ^^

c'est le plus intéressant

par **nuage** » 15 Juil 2008, 15:53

Salut,
comme le dit ThSQ pour la démonstration il suffit de calculer le «volume» d'un simplexe de dimension n.
On a ensuite la probabilité d'avoir besoin de n tirages.
Et la suite est la définition de l'exponentielle par une série entière

par **Imod** » 15 Juil 2008, 16:05

Le volume du simplexe étant donné par :

Imod

par **_-Gaara-_** » 15 Juil 2008, 19:06

Comme deux solutions valent mieux qu'une :

http://www.physics.harvard.edu/academics/undergrad/probweek/sol38.pdf

bien joué, les gars :++:

mais à mon niveau je ne pourrais pas me permettre de dire "il suffit de.. " xD ^^

par **nuage** » 15 Juil 2008, 19:25

Salut,

_-Gaara-_ a écrit:[...]mais à mon niveau je ne pourrais pas me permettre de dire "il suffit de.. " xD ^^

Bien sur.
Mais quand je dis « il suffit de calculer » ça ne veut pas dire que l'on peut se dispenser du calcul.
De même le résultat donné par imod mérite une démonstration.
Qui peut se faire, à un niveau élémentaire, par récurrence.

Pour finir j'ai trouvé ton problème agréable, et son résultat surprenant.

Défi Enigme

Défi Enigme

Qui est en ligne