Topologie !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 21 Sep 2007, 14:40
Bonjour :
Je voudrai que vous m'aidiez à comprendre la démonstration de l'exercice suivant :
Soit
 $)
un espace topologique quelconque.
Soit :
.
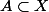
Soit :
.
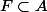
Montrer que :
est un fermé de
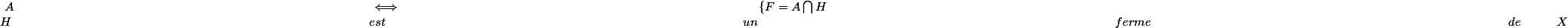
Voiçi la demonstration de cet exercice :
est un fermé de
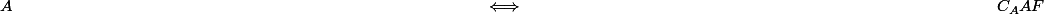
est un ouvert de
.
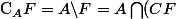 \hspace{10cm} \Longleftrightarrow \hspace{10cm} A \bigcap (C F) = A \bigcap W $)
et
est un ouvert de
 $)
Pourquoi
est un ouvert de
Voiçi la suite :
 = X \hspace{10cm} \Longrightarrow \hspace{10cm} (A \bigcap F) \bigcup (A \bigcap (CF))=A \hspace{10cm} \Longrightarrow \hspace{10cm} F\bigcup(A\bigcap(CF))=A$)
 $)
 = X \hspace{10cm} \Longrightarrow \hspace{10cm} (W \bigcap A ) \bigcup ( A \bigcap (CW) ) = A \hspace{10cm} \Longrightarrow \hspace{10cm} ((CF)\bigcap A) \bigcup (A\bigcap(CW)) = A $)
 $)
Par conséquent :
 = F $)
et donc
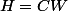
qui un fermé de
Voilà .. ! c'est tout ce que j'ai à vous poser comme question, j'avais une autre question à vous poser, mais au moment ou je tapais ce message sur le net , j'ai trouvé pourquoi .. , la question était pourquoi :
... mais c'est clair maintenant d'après
 $)
et
 $)
Merci d'avance de votre aide !
par legeniedesalpages » 21 Sep 2007, 14:51
Bonjour, par définition un ouvert de A est l'intersection d'un ouvert W de X avec A.
Ici
)
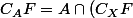est ouvert dans A, donc il existe un ouvert W de X tel que
 = A\cap W)
.
Réciproquement si il existe un ouvert W de X tel que
, alors
est un ouvert de A.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
par fahr451 » 21 Sep 2007, 14:51
bonjour
la topologie induite par X sur sur A est la suivante par définition
les ouverts de A sont exactement les traces sur A des ouverts de X
c'est a dire les O inter A
avec O ouvert de X
ton exo est montrer que le s fermés de A sont exactement les traces sur A des fermés de X c'est à dire les H inter A avec H fermé de X
ce qui se fait bien sûr par passage au complémentaire
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 21 Sep 2007, 15:06
Merci beaucoup "fahr451" et "legeniedesalpages" !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 14:36
Bonjour :
Est ce que vous savez comment trouver le corrigés du document suivant sur le net :
[url=http://]http://saralegi.free.fr/Enseignement/ExercicesTopologie.pdf[/url]
Merci infiniment !!
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 30 Sep 2007, 14:39
Tu sais Barbu, Saralegi, c'est mon prof de topo :)
C'est marrant comme le monde est petit lol :)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 14:46
:jap: :king:
Tu peux lui demander qu'il te donne le corrigé de ce document ??
:+++:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 30 Sep 2007, 14:47
ça ferait suspect non ???
On est entrain de faire ces exos en TD xD
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 23:25
Bonsoir :
Voiçi un exercice qui semble facile à resoudre, mais ma tête ne fonctionne pas bien cette nuit !! :hum: ..Est ce que vous pouvez m'aider ?!
Montrer que :
 \subset \displaystyle \bigcap_{n \in \mathbb{N}} Int(A_{n}) $)
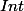
: signifie l'interieur de ... ( ... d'un ensemble )
Merci infiniment !!
par legeniedesalpages » 30 Sep 2007, 23:29
l'intérieur d'une partie d'un espace topologique plutôt
Bonsoir au fait :)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
par fahr451 » 30 Sep 2007, 23:31
bonsoir
l'ensemble de droite est un ouvert
il est inclus dans l intersection des An donc dans chaque An
donc dans l'intérieur de chaque An (car l'intérieur de An est le plus grand ouvet inclus dans An)
donc ds l'intersecrion des intérieurs
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 23:39
Ah non mais c'est très simple, il suffit d'écrire :
Soit
 $)
Alors :
 \hspace{10cm} \Longrightarrow \hspace{10cm}<br />\exists O \in \mathcal{T} \hspace{10cm} : \hspace{10cm} x \in O \subset \displaystyle \bigcap_{n \in \mathbb{N}} A_{n} \hspace{10cm} \Longrightarrow \hspace{10cm} \forall n \in \mathbb{N} \hspace{10cm} : \hspace{10cm} x \in O \subset A_{n} \hspace{10cm} \Longrightarrow \hspace{10cm} \forall n \in \mathbb{N} \hspace{10cm} : \hspace{10cm} A_{n} \in \upsilon(x) \hspace{10cm} \Longrightarrow \hspace{10cm} \forall n \in \mathbb{N} \hspace{10cm} x \in Int(A_{n}) \hspace{10cm} \Longrightarrow \hspace{10cm} x \in \displaystyle \bigcap_{ n \in \mathbb{N}} Int(A_{n}) $)
CQFD !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 23:41
Merci pour vos reponses !
-
mejdane
- Membre Naturel
- Messages: 51
- Enregistré le: 01 Aoû 2006, 23:08
-
par mejdane » 30 Sep 2007, 23:41
soit x appartenant à l'intersection des Int( An),donc il existe r>0 tq ]x-r,x+r[ inclus ds intersection An, donc pour tt n ]x-r,x+r[ inclus ds An donc pour tt n x appartiend à Int(An) d'où:
x appartiend à intersection (Int(An)!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 23:52
et celle là ? :
!
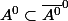
Merci infiniment !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 30 Sep 2007, 23:53
Il suffit de montrer que
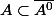
et ensuite déduire la relation !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 01 Oct 2007, 00:13
Soit x \in A
Il faut montrer que :
 \hspace{10cm} : \hspace{10cm} V \bigcap A^{0} \neq \empty $)
Or c'est pas toujours le cas !!
Comment faire pour montrer cette petite formule ?
Merci d'avance de votre aide !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 01 Oct 2007, 23:31
Help pls !! :mur:
par legeniedesalpages » 01 Oct 2007, 23:47
Bonsoir Barbu,
si x est dans A-ronde c'est évident,
si x n'est pas dans A-ronde, d'après ce que tu as dit Hier à 00h53(je ne suis pas sûr de ça mais bon je te crois) alors x est quand même dans l'adhérence de A-ronde, donc tout voisinage de x rencontre A-ronde.
par legeniedesalpages » 01 Oct 2007, 23:49
sinon pour ce que tu as dit hier à 00:52, je procèderais plutôt comme ça,
A-ronde est dans son adhérence et est ouvert, donc il est dans l'intérieur de son adhérence.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
