Topologie !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Oct 2007, 23:33
par barbu23 » 03 Oct 2007, 23:33
legeniedesalpages a écrit:non je ne dis pas le contraire mais la frontière de A est incluse dans A si et seulement si A est fermé.
tu prends la boule ouverte unité, sa frontière sera la sphère unité, et ces deux parties sont disjointes, et donc la sphère unité n'est pas dans la boule ouverte unité.
oui, c'est vrai !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Oct 2007, 23:40
par barbu23 » 03 Oct 2007, 23:40
barbu23 a écrit:Soient
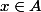
et
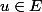
avec :
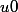
:
On considère l'ensemble :
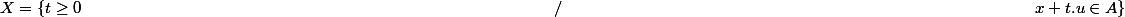
.
Montrer que
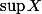
existe .
Pour montrer que
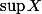
existe, il faut montrer que

est non vide et majorée !!
Pour

non vide, c'est clair !! il suffit de prendre
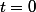
car :
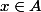
Pour

majorée, je ne vois pas encore comment proceder !!
 par legeniedesalpages » 03 Oct 2007, 23:57
par legeniedesalpages » 03 Oct 2007, 23:57
ok donc on doit avoir pour tout
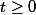
,
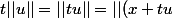-x||\leq diam(A))
, donc
}{||u||})
.
Par conséquent

est majoré.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Oct 2007, 23:59
par barbu23 » 03 Oct 2007, 23:59
barbu23 a écrit: $)
Montrer que :
) \leq diam(A) $)
.
Moi, je pense que même si :

( inclusion seulement dans le sens direct ) .. on a:
 = diam(A) = diam(\overline{A}) $)
... parcequ'il s'agit de borne superieure et par exemple dans
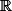
la borne superieure d'un ouvert est la même que celui d'un fermé ...
Est ce que tu as un contre exemple, sinon il faut le demontrer !!
et celà evidemment peut nous aider à montrer la question
 $)
qui te pose problème !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:01
par barbu23 » 04 Oct 2007, 00:01
legeniedesalpages a écrit:ok donc on doit avoir pour tout
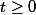
,
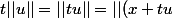-x||\leq diam(A))
, donc
}{||u||})
.
Par conséquent

est majoré.
oui, jolie astuce !! :lol2:
 par legeniedesalpages » 04 Oct 2007, 00:07
par legeniedesalpages » 04 Oct 2007, 00:07
barbu23 a écrit:Moi, je pense que même si :

( inclusion seulement dans le sens direct ) .. on a:
 = diam(A) = diam(\overline{A}) $)
... parcequ'il s'agit de borne superieure et par exemple dans
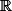
la borne superieure d'un ouvert est la même que celui d'un fermé ...
Est ce que tu as un contre exemple, sinon il faut le demontrer !!
et celà evidemment peut nous aider à montrer la question
 $)
qui te pose problème !!
je pense que l'on peut considérer
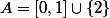
et
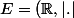)
Ici
<diam(A))
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:11
par barbu23 » 04 Oct 2007, 00:11
 $)
En déduire que toute demi-droite issue d'un point

de

coupe
 $)
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:18
par barbu23 » 04 Oct 2007, 00:18
celà veut dire qu'il faut vérifier que :
 = (\{ t \geq 0\hspace{10cm} / \hspace{10cm} x + t.u \in A \}) \bigcap Fr(A) \neq \empty $)
 par legeniedesalpages » 04 Oct 2007, 00:20
par legeniedesalpages » 04 Oct 2007, 00:20
barbu23 a écrit:celà veut dire qu'il faut vérifier que :
 = (\{ t \geq 0\hspace{10cm} / \hspace{10cm} x + t.u \in A \}) \bigcap Fr(A) \neq \empty $)
ok mais alors pour vérifier, je vois même pas d'où partir :triste:
 par legeniedesalpages » 04 Oct 2007, 00:28
par legeniedesalpages » 04 Oct 2007, 00:28
ah peut être essayer de montrer que
u\in Fr(A))
(

dépendant de

et de

).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:34
par barbu23 » 04 Oct 2007, 00:34
legeniedesalpages a écrit:ah peut être essayer de montrer que
u\in Fr(A))
(

dépendant de

et de

).
oui, bonne idée .. en montrant ,par absurde, que :
.u \not \in A^{0} $)
 par legeniedesalpages » 04 Oct 2007, 00:35
par legeniedesalpages » 04 Oct 2007, 00:35
barbu23 a écrit:oui, bonne idée .. en montrant ,par absurde, que :
.u \not \in A^{0} $)
tu voulais dire
.u \in A^{0})
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:45
par barbu23 » 04 Oct 2007, 00:45
On veut montrer que :
 .u \in Fr(A) = \overline{A} \backslash A^{0} $)
Celà signifie qu'il faut montrer que
 .u \in \overline{A} $)
et
 .u \not \in A^{0}$)
.
 .u \in \overline{A} $)
est toujours verifié.
Il reste à montrer que
 .u \not \in A^{0}$)
.
Et là, on procède par absurde, on suppose que
 .u \in A^{0}$)
et on cherche une contradiction !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:49
par barbu23 » 04 Oct 2007, 00:49
On suppose que
.u \in A^{0} $)
Alors , il existe un ouvert

de

tel que :
.u \in O \subset A $)
Il faut trouver un
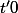
tel que :
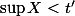
et
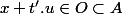
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 00:53
par barbu23 » 04 Oct 2007, 00:53

n'est malheureusement pas un ensemble ordonnée !
 par legeniedesalpages » 04 Oct 2007, 01:01
par legeniedesalpages » 04 Oct 2007, 01:01
Bon donc on raisonne par l'absurde:
on suppose qu'il existe une demi-droite issue d'un point

de

:
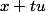
, telle que
u\in A^0)
.
on note
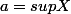
,
on a une suite

de

qui tend vers

.
Donc comme
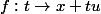
est continue,
)
tend vers
=x+au)
.
On remarque que
)
est dans
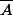
.
Comme
)
est dans
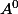
par hypothèse, il existe une boule ouverte
,r))
, de centre
)
et de rayon
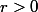
.
On a
u\in B(f(a),r)\subset A)
, donc
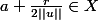
, ce qui est absurde,
Donc
)
est dans la frontière de

.
Edit: je vais aller me coucher, bonne nuit :dodo:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Oct 2007, 01:12
par barbu23 » 04 Oct 2007, 01:12
:++: :++: :++: :++: :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
