Topologie !

par **barbu23** » 03 Oct 2007, 22:43

Voiçi un exo sur les diamètres :
Soit :

un espace vectoriel normé.
Soit

une partie non vide et bornée de

.
On définit :

Montrer que si

est bornée alors

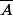
et

sont bornés.

par **legeniedesalpages** » 03 Oct 2007, 22:48

déjà si on arrive à montrer que

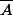
est bornée alors

est bornée, puisque

.

par **legeniedesalpages** » 03 Oct 2007, 22:50

c'est un evn sur R ou C, ou ça peut être encore sur autre chose?

E est de dimension finie ou pas forcément?

par **barbu23** » 03 Oct 2007, 22:54

est de dimension finie sur

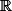
par **legeniedesalpages** » 03 Oct 2007, 22:57

ok alors on peut voir avec la caractérisation séquentielle de l'adhérence peut être.

par **barbu23** » 03 Oct 2007, 23:04

si

alors :

car

est un fermé !!
CQFD .

par **barbu23** » 03 Oct 2007, 23:07

Comparer

,

et

lorsque

par **legeniedesalpages** » 03 Oct 2007, 23:11

oui ce que j'étais en train de penser pour la 1) aussi, mais avec

.

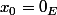
En fait c'est la définition d'ensemble borné dans un evn que j'avais eu dans un cours de calcul diff je crois

par **legeniedesalpages** » 03 Oct 2007, 23:13

pour la 2), on a

, vu que

.

par **barbu23** » 03 Oct 2007, 23:15

absolument, c'est très facile !! :+++:

par **barbu23** » 03 Oct 2007, 23:16

oui mais je vois pas pourquoi il ont ajouté la condition que

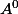
est non vide !!

par **barbu23** » 03 Oct 2007, 23:18

Montrer que :

.

par **barbu23** » 03 Oct 2007, 23:18

Montrer que :

.

par **barbu23** » 03 Oct 2007, 23:20

par **legeniedesalpages** » 03 Oct 2007, 23:22

ben sinon

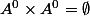
, et si tu notes

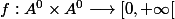
qui à tout

associe

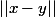
, tu auras alors

.
Et ça pose ensuite problème car le sup n'est pas défini pour l'ensemble vide.

D'autre part, si

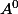
est non vide, alors

et

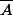
sont alors aussi non vide, et on évite aini le même problème.

par **legeniedesalpages** » 03 Oct 2007, 23:25

barbu23 a écrit:

cette implication est vraie, mais par contre

n'est pas toujours vraie.

par **barbu23** » 03 Oct 2007, 23:27

Soient

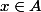
et

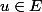
avec :

:
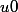
On considère l'ensemble :

.
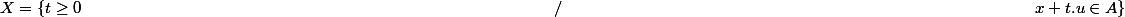
Montrer que

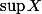
existe .

par **barbu23** » 03 Oct 2007, 23:29

L'execice est encore long, et on finit par demontrer que l'égalité existe !! ( donc, toi tu dis le contraire, je ne sais pas encore ! )

par **legeniedesalpages** » 03 Oct 2007, 23:30

non je ne dis pas le contraire mais la frontière de A est incluse dans A si et seulement si A est fermé.

tu prends la boule ouverte unité, sa frontière sera la sphère unité, et ces deux parties sont disjointes, et donc la sphère unité n'est pas dans la boule ouverte unité.

par **barbu23** » 03 Oct 2007, 23:31

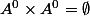
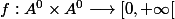
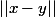
legeniedesalpages a écrit:ben sinon , et si tu notes qui à tout associe , tu auras alors .
Et ça pose ensuite problème car le sup n'est pas défini pour l'ensemble vide.

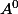
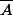
D'autre part, si est non vide, alors et sont alors aussi non vide, et on évite aini le même problème.

oué, c'est vrai tu as raison j'ai pas reflechi à ça !! :mur: :lol2:

Topologie !

Qui est en ligne