Topologie (révision)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par sandrine_guillerme » 26 Aoû 2007, 01:53
barbu23 a écrit:Sandrine, bonsoir :
Tu peux commencer par remarquer Que
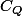
est dense dans
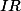
, donc
,
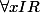
qui est un fermé n'est ce pas ?! donc il existe une suite
_{n \in IN} $)
tel que:
.
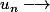
Alors, je te laisse conclure !!
Salut barbu,
ce que tu viens de dire c'est la définition de la densité,
on a l'adhérence de l'ensemble des irrationnels est R, qui est un fermé (et ouvert aussi) mais je ne vois donc pas comment faire le lien,
peut être que j'étais pas claire, en fait, le but de mon exercice c'était de trouver un x (réel) dont la distance à cette partie n'est atteinte en aucun point de
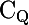
.. et j'ai donc pensé à calculer la distance de x à
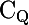
.. Suis je d'abord sur la bonne voie ?
par sandrine_guillerme » 26 Aoû 2007, 02:12
barbu23 a écrit: est inlus dans
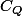
biensûr !!
Je crois que j'ai compris ce que tu veux dire .. !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 19:04
par barbu23 » 26 Aoû 2007, 02:20
Salut Sandrine :
On trouve ;dans n'importe quel cours de topologie ;niveau L3, la proposition suivante :
Soit
 $)
un espace metrique muni biensûr de la distance usuelle
.
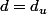
Soit :
.
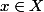
est une valeur d'adhérence de
( c'est à dire :
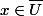
) si et seulement si
_{n \in IN} \subset U $)
telle que :
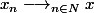
C'est ce que moi j'ai appliqué pour le cas de ton exercice :
On a :
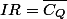
, donc tous point de
:
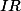
est dans l'adherence de
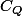
..donc d'après la proposition que j't'ai cité çi-dessus :
_{n \in IN} \subset C_Q $)
telle que :
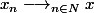
c'est à dire :
 = 0 $)
Donc, qu'est ce qu'on peut conclure là, quelque soit le point
dont tu parles dans
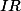
, la distance entre
et l'ensemble des irrationnels est nul .
Voilà .. !
par sandrine_guillerme » 26 Aoû 2007, 02:29
C'est exactement ce que j'avais compris dans ta phrase ..
Merci barbu :smoke2:
Donc là je cherche le réel x dont la distance à cette partie n'est atteinte en aucun point de
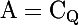
i.e pour le quel il n'existe aucun point y tq d(x,A) = d(x,y)
J'en vois pas là moi .
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 19:04
par barbu23 » 26 Aoû 2007, 03:17
Je comprends pas exactement ce que tu cherches :marteau: :
 = 0 $)
, donc tu cherches
tel qu'il n'existe aucun
tel que
 = 0 $)
, c'est à dire tu cherches
tel que
:
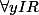
 \neq 0 $)
, et ben ça doit être un point dans le complementaire de
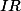
qui est
.
Est ce que c'est bien ça ce que tu cherches ?!
par sandrine_guillerme » 26 Aoû 2007, 03:22
Tout à fait !
La question était bien évidement assez chelou mais j'ai compris ..
Merci barbu !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
