Topologie !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 01:08
par barbu23 » 02 Oct 2007, 01:08
:++:
La tienne est plus courte et intelligente .. !
la prochaine fois, je vais appliquer la même astuce que toi .. !! :lol2:
 par legeniedesalpages » 02 Oct 2007, 01:11
par legeniedesalpages » 02 Oct 2007, 01:11
en fait je me souvenais qu'en topologie, pour certaines démos tu manipules les images réciproques et la continuité.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 01:12
par barbu23 » 02 Oct 2007, 01:12
Et celle là : ( c'est pas évident je pense )
 \subset \overline{f(A)} $)
avec les mêmes conditions que l'exercice precedent (
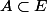
)
 par legeniedesalpages » 02 Oct 2007, 01:12
par legeniedesalpages » 02 Oct 2007, 01:12
bon je vais me coucher, à plus pour une séance topo :lol2:
Bonne nuit :)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 01:14
par barbu23 » 02 Oct 2007, 01:14

est par hypothèse, dans
} $)
 par legeniedesalpages » 02 Oct 2007, 01:15
par legeniedesalpages » 02 Oct 2007, 01:15
lol allez une dernière pour celle là il y a même:
f est continue si et seulement si pour tout
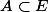
,
\subset \overline{f(A)})
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 01:15
par barbu23 » 02 Oct 2007, 01:15
D'accord :lol2: bonne nuit !!
 par legeniedesalpages » 02 Oct 2007, 01:18
par legeniedesalpages » 02 Oct 2007, 01:18
pour l'implication directe, il faut que tu utilises le fait que
))
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 01:29
par barbu23 » 02 Oct 2007, 01:29
legeniedesalpages a écrit:pour l'implication directe, il faut que tu utilises le fait que
))
.
Je ne vois encore ou ça peut servir
))
.
 par legeniedesalpages » 02 Oct 2007, 09:55
par legeniedesalpages » 02 Oct 2007, 09:55
On a
)\subset f^{-1}(\overline{f(A)}))
.
Comme

est continue,
}))
est fermé,
d'où
}))
, et donc
 \subset \overline{f(A)})
.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 18:02
par barbu23 » 02 Oct 2007, 18:02
oui, tu as raison "legeniedesalpages" , merci pour ta reponse !!
 par legeniedesalpages » 02 Oct 2007, 19:52
par legeniedesalpages » 02 Oct 2007, 19:52
reste la réciproque à montrer, tu l'as trouvé?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 21:31
par barbu23 » 02 Oct 2007, 21:31
Soit
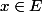
Soit
) $)
Il faut trouver un
 $)
tel que :
 \subset V $)
C'est pas encore evident pour moi !!
 par legeniedesalpages » 02 Oct 2007, 21:35
par legeniedesalpages » 02 Oct 2007, 21:35
il est plus pratique d'utiliser la caractérisation de la continuité en termes de fermés et d'image réciproque.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 22:39
par barbu23 » 02 Oct 2007, 22:39
Soit

un fermé de

.
On a, par hypothèse,
}) \subset \overline{f(f^{-1}(B))} \subset \overline{B} = B $)

})) \subset f^{-1}(B) $)
Et puisque :
} \subset f^{-1}(f(\overline{f^{-1}(B)})) $)
Alors :
} \subset f^{-1}(B) $)
Et puisque :
 \subset \overline{f^{-1}(B)} $)
Alors :
 = \overline{f^{-1}(B)} $)
Par conséquent :
 $)
est fermé !
CQFD.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 02 Oct 2007, 22:43
par barbu23 » 02 Oct 2007, 22:43
Il a fallu du temps pour touver la solution !! c'est pas facile du tout !!
:king:
 par legeniedesalpages » 02 Oct 2007, 22:56
par legeniedesalpages » 02 Oct 2007, 22:56
oui cette équivalence est pas évidente à montrer, c'est difficili de s'y retrouver dans ce jonglage d'images réciproques et de fermés.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 03 Oct 2007, 22:15
par barbu23 » 03 Oct 2007, 22:15
Bonsoir "legeniedesalpages" :
Ou est ce qu'on est arrivé en Topologie ? :lol2:
 par legeniedesalpages » 03 Oct 2007, 22:19
par legeniedesalpages » 03 Oct 2007, 22:19
Bonsoir, je crois que c'était les inclusions d'images/préimages de fonctions continues, non? :langue2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
