Questions de cours sur les lois internes, groupes, anneaux e
Ce qui est dommage avec ce genre de cours c'est qu'à part des définitions on ne sait finalement rien de ces structures alors qu'elles ont une foule de propriétés intéressantes. Je me rappelle en sup, on a d'abord vu les groupes avec les complexes et les racines de l'unité. Quand on a fait les polynômes on a vu les anneaux et un peu plus loin les corps avec les Z/pZ etc. C'était assez agréable car on sentait vraiment l'utilité de ces notions.
Nightmare a écrit:Ce qui est dommage avec ce genre de cours c'est qu'à part des définitions on ne sait finalement rien de ces structures alors qu'elles ont une foule de propriétés intéressantes. Je me rappelle en sup, on a d'abord vu les groupes avec les complexes et les racines de l'unité. Quand on a fait les polynômes on a vu les anneaux et un peu plus loin les corps avec les Z/pZ etc. C'était assez agréable car on sentait vraiment l'utilité de ces notions.
bonjour
j abonde en précisant qu'une illustration majeure des groupes est celle des groupes de transformations
par exemple
ensemble des isométries affines planes qui laissent stable un carré ; un triangle
Bon, je me lance.
Soit G un groupe quelconque, soient A et B deux sous-groupes de G pour la même loi.
On suppose que la réunion de A et de B, notée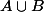 est un sous-groupe de G, et que B ne contienne pas A. Si cette hypothèse est juste, alors il existe donc un a dans A qui ne soit pas dans B. On va montrer que ce n'est pas le cas, et donc que B est inclus dans A.
est un sous-groupe de G, et que B ne contienne pas A. Si cette hypothèse est juste, alors il existe donc un a dans A qui ne soit pas dans B. On va montrer que ce n'est pas le cas, et donc que B est inclus dans A.
Soit b dans B, alors ab est dans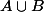 (par stabilité du produit), mais ab n'est pas contenu dans B parce que dans ce cas-ci on aurait
(par stabilité du produit), mais ab n'est pas contenu dans B parce que dans ce cas-ci on aurait b^{-1} \in B) .
.
Donc ab est forcément dans A, d'oùa^{-1} \in A) (stabilité par passage à l'inverse).
(stabilité par passage à l'inverse).
On en déduit que le groupe G ne peut être la réunion de deux sous-groupes (autres que les deux sous-groupes {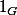 } et G lui-même).
} et G lui-même).
Je ne sais pas si je réponds à la question, j'ai l'impression de m'être égaré :hein:
Soit G un groupe quelconque, soient A et B deux sous-groupes de G pour la même loi.
On suppose que la réunion de A et de B, notée
Soit b dans B, alors ab est dans
Donc ab est forcément dans A, d'où
On en déduit que le groupe G ne peut être la réunion de deux sous-groupes (autres que les deux sous-groupes {
Je ne sais pas si je réponds à la question, j'ai l'impression de m'être égaré :hein:
T'es sur la bonne voie mais c'est la phrase
qui est fausse. La conclusion de ta démo c'est que B est contenu dans A. T'as montré donc que A U B est un groupe implique A C B ou B C A
Timothé Lefebvre a écrit:
On en déduit que le groupe G ne peut être la réunion de deux sous-groupes (autres que les deux sous-groupes {} et G lui-même).
qui est fausse. La conclusion de ta démo c'est que B est contenu dans A. T'as montré donc que A U B est un groupe implique A C B ou B C A
Timothé Lefebvre a écrit:Soit b dans B [...] d'où(stabilité par passage à l'inverse).
On en déduit que le groupe G ne peut être la réunion de deux sous-groupes (autres que les deux sous-groupes {} et G lui-même).
Je sais pas comment diable t'as fait cette déduction, moi, de "pour tout b dans B, b est dans A", je déduis plutôt que B est inclus dans A, mais c'est tout.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
