Polynômes irréductibles Z/pZ[X]
23 messages
- Page 1 sur 2 - 1, 2
Polynômes irréductibles Z/pZ[X]
Bonjour à tous,
j'aurais aimé savoir comment déterminer les polynômes irréductibles dans les anneaux de la forme Z/pZ[X] où p est un nombre premier.
Pour des nombres premiers "p" pas trop grands j'ai cru comprendre qu'il y avait des techniques pour les voir rapidement, par exemple en sachant d'entrée de jeu de combien de monômes le polynôme sera composé.
Si je demande par exemple quels sont les polynômes irréductibles de degré 3 dans Z/3Z[X]?
Merci par avance,
j'aurais aimé savoir comment déterminer les polynômes irréductibles dans les anneaux de la forme Z/pZ[X] où p est un nombre premier.
Pour des nombres premiers "p" pas trop grands j'ai cru comprendre qu'il y avait des techniques pour les voir rapidement, par exemple en sachant d'entrée de jeu de combien de monômes le polynôme sera composé.
Si je demande par exemple quels sont les polynômes irréductibles de degré 3 dans Z/3Z[X]?
Merci par avance,
Re: Polynômes irréductibles Z/pZ[X]
Bonjour
Si est petit, le plus rapide est d'écrire les réductibles (produits de polynômes de degré strictement inférieur) et de chercher qui n'est pas apparu. On peut avoir une minoration du nombre des réductibles. Si
est petit, le plus rapide est d'écrire les réductibles (produits de polynômes de degré strictement inférieur) et de chercher qui n'est pas apparu. On peut avoir une minoration du nombre des réductibles. Si  est plus grand, il existe des méthodes, comme le critère d'Eisenstein par exemple, mais de toute façon c'est compliqué.
est plus grand, il existe des méthodes, comme le critère d'Eisenstein par exemple, mais de toute façon c'est compliqué.
Un polynôme de degré 3, est réductible si et seulement si il a au moins une racine dans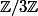 . Je te laisse vérifier que
. Je te laisse vérifier que 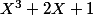 convient.
convient.
Si
Un polynôme de degré 3, est réductible si et seulement si il a au moins une racine dans
Re: Polynômes irréductibles Z/pZ[X]
Salut,
Sur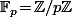 il y a une façon simple de trouver les irréductibles de degré
il y a une façon simple de trouver les irréductibles de degré  donné ou de tester si un polynôme est irréductible vu que, si
donné ou de tester si un polynôme est irréductible vu que, si 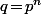 , le polynôme
, le polynôme 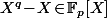 est le produit de tout les polynôme irréductible de
est le produit de tout les polynôme irréductible de 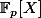 dont le degré
dont le degré  divise
divise  .
.
En particulier un polynôme de degré est irréductible ssi il divise
est irréductible ssi il divise 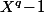 .
.
Par exemple, sur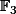 ,
,
- Le produit de tout les polynômes irréductible de degré 1 est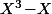 donc il y en a 3.
donc il y en a 3.
- Le produit de tout les polynômes irréductible de degré 2 est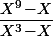 donc il y en a (9-3)/2=3.
donc il y en a (9-3)/2=3.
- Le produit de tout les polynômes irréductible de degré 3 est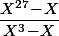 donc il y en a (27-3)/3=8.
donc il y en a (27-3)/3=8.
- Le produit de tout les polynômes irréductible de degré 4 est\!\times\!\dfrac{X^9\!-\!X}{X^3\!-\!X}}=\dfrac{X^{81}\!-\!X}{X^9\!-\!X}) donc il y en a (81-9)/4=18.
donc il y en a (81-9)/4=18.
- Le produit des polynômes irréductible de degré 6 est\!\times\!\dfrac{X^9\!-\!X}{X^3\!-\!X}\!\times\!\dfrac{X^{27}\!-\!X}{X^3\!-\!X}}=\dfrac{(X^{729}\!-\!X)(X^{3}\!-\!X)}{(X^9\!-\!X)(X^{27}\!-\!X)}) donc il y en a (729+3-9-27)/6=116.
donc il y en a (729+3-9-27)/6=116.
etc...
Sur
En particulier un polynôme de degré
Par exemple, sur
- Le produit de tout les polynômes irréductible de degré 1 est
- Le produit de tout les polynômes irréductible de degré 2 est
- Le produit de tout les polynômes irréductible de degré 3 est
- Le produit de tout les polynômes irréductible de degré 4 est
- Le produit des polynômes irréductible de degré 6 est
etc...
Modifié en dernier par Ben314 le 08 Jan 2017, 20:33, modifié 5 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes irréductibles Z/pZ[X]
Mimosa a écrit:Bonjour
Siest petit, le plus rapide est d'écrire les réductibles (produits de polynômes de degré strictement inférieur) et de chercher qui n'est pas apparu. On peut avoir une minoration du nombre des réductibles. Si
est plus grand, il existe des méthodes, comme le critère d'Eisenstein par exemple, mais de toute façon c'est compliqué.
Un polynôme de degré 3, est réductible si et seulement si il a au moins une racine dans. Je te laisse vérifier que
convient.
Bonjour Mimosa,
merci pour ta réponse,
ta méthode est très bien, je l'ai utilisée, mais je me demandais si il y avait qqch de trivial qui m'avait échappé car en td j'ai remarqué que beaucoup d'élèves balançaient les 3 ( je crois qu'ils sont 3 ) polynômes irréductibles de tête et en moins de 15 secondes, et sans pour autant les avoir retenu de mémoire, du moins il me semble...
Re: Polynômes irréductibles Z/pZ[X]
Ben314 a écrit:Salut,
Suril y a une façon simple de trouver les irréductibles de degré
donné ou de tester si un polynôme est irréductible vu que, si
, le polynôme
est le produit de tout les polynôme irréductible de
dont le degré
divise
.
En particulier un polynôme de degréest irréductible ssi il divise
.
Salut Ben,
merci pour ta réponse,
oui j'ai ce théorème aussi dans mon cours, d'ailleurs ce ne serait pas plutôt - X au lieu de moins 1 dans ta formule?
Re: Polynômes irréductibles Z/pZ[X]
ahah ok, le temps que je réponde tu as déjà corrigé, merci pour ton exemple je vais regarder cela tout de suite
Re: Polynômes irréductibles Z/pZ[X]
Non, il y en a 8 : c.f. le post précédent que j'ai complété.yoshi13 a écrit:...en td j'ai remarqué que beaucoup d'élèves balançaient les 3 ( je crois qu'ils sont 3 ) polynômes irréductibles...
Modifié en dernier par Ben314 le 08 Jan 2017, 20:40, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes irréductibles Z/pZ[X]
Oui tout a fait , l'histoire où les mecs ont trouvé 3 polynôme de degré 3 rapidement ca devait être sur F2, merci pour tes exemples , ca éclaircit beaucoup de choses
Re: Polynômes irréductibles Z/pZ[X]
Même sur F3, c'est super rapide pour les degrés <= 3, vu que, comme le dit Mimosa, dans ce cas on a :
Irréductible <=> Sans Racines (ce qui est évidement faux à partir du degré 4).
Donc ce sont eux de la forme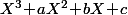 tels que
tels que 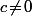 ,
, 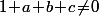 et
et 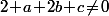 .
.
Et ça va super vite d'en dresser la liste (mais la formule théorique du post précédent te permet bien plus rapidement de voir qu'il y en a 8)
Irréductible <=> Sans Racines (ce qui est évidement faux à partir du degré 4).
Donc ce sont eux de la forme
Et ça va super vite d'en dresser la liste (mais la formule théorique du post précédent te permet bien plus rapidement de voir qu'il y en a 8)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes irréductibles Z/pZ[X]
Merci, c'est excellent comme technique, je passe encore un peu de temps à déterminer les polynômes irréductibles ( après savoir combien j'en cherche du coup )
J'imagine qu'il doit y avoir un moyen de résolution pour déterminer les a,b,c etc.. en fonction des conditions que tu as énoncées , cad c=/=0, 1+a+b+c=/=0 etc...
J'ai essayé des trucs mais rien de bien convainquant
Il doit y avoir un moyen à l'aide de matrices, ou de système de résolution d'équations d'inconnues a,b,c, etc.. selon le degré du polynôme étudié?
J'imagine qu'il doit y avoir un moyen de résolution pour déterminer les a,b,c etc.. en fonction des conditions que tu as énoncées , cad c=/=0, 1+a+b+c=/=0 etc...
J'ai essayé des trucs mais rien de bien convainquant
Il doit y avoir un moyen à l'aide de matrices, ou de système de résolution d'équations d'inconnues a,b,c, etc.. selon le degré du polynôme étudié?
Re: Polynômes irréductibles Z/pZ[X]
Attention : Il n'y a pas de "etc..." vu que irréductible <=> sans racines uniquement pour les degré inférieur ou égaux à 3 donc à partir du degré 4, ça ne suffit pas d'écrire que P(0)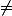 0, P(1)
0, P(1)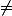 0...
0...
A la limite, tu peut dresser la liste de tels polynômes puis, après avoir dressé la liste des irréductibles de degré 2, éliminer ceux qui sont divisible par un irréductible de degré 2. Mais ça commence à être fastidieux (et je te dit pas au delà)
Bref, normalement, cette "astuce", ça se limite au degré 3 (*) et vu que c'est des inégalités et pas des égalités qu'il y a à résoudre, je pense pas que l'algèbre linéaire (i.e. les systèmes) aient un grand intérêt pour la résolution.
En plus, vu qu'il y en a un "gros paquet" (précisément (p^3-p)/3 sur Fp) si tu veut tous les écrire et ne pas te contenter des p inégalités obtenues, ce qui est long, c'est pas les calculs, c'est bêtement de les écrire !!!!
(*) ou 2, mais pour ceux de degré 2, il y a plus simple : il suffit de dire que le discriminant ne doit pas être un carré du corps en question.
A la limite, tu peut dresser la liste de tels polynômes puis, après avoir dressé la liste des irréductibles de degré 2, éliminer ceux qui sont divisible par un irréductible de degré 2. Mais ça commence à être fastidieux (et je te dit pas au delà)
Bref, normalement, cette "astuce", ça se limite au degré 3 (*) et vu que c'est des inégalités et pas des égalités qu'il y a à résoudre, je pense pas que l'algèbre linéaire (i.e. les systèmes) aient un grand intérêt pour la résolution.
En plus, vu qu'il y en a un "gros paquet" (précisément (p^3-p)/3 sur Fp) si tu veut tous les écrire et ne pas te contenter des p inégalités obtenues, ce qui est long, c'est pas les calculs, c'est bêtement de les écrire !!!!
(*) ou 2, mais pour ceux de degré 2, il y a plus simple : il suffit de dire que le discriminant ne doit pas être un carré du corps en question.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes irréductibles Z/pZ[X]
Si tu veut, je te le fait sur F3 pour que tu voit bien que c'est vraiment pas les calculs qui sont long.
On cheche donc tout les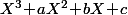 tels que
tels que 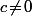 ,
, 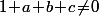 et
et 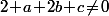 .
.
(1) Si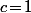 on doit avoir
on doit avoir 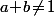 et
et 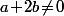 :
:
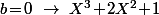
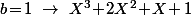
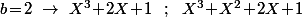
(2) Si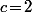 on doit avoir
on doit avoir 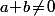 et
et 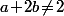 :
:
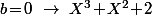
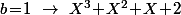
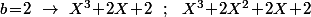
On cheche donc tout les
(1) Si
(2) Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes irréductibles Z/pZ[X]
Ben314 a écrit:Si tu veut, je te le fait sur F3 pour que tu voit bien que c'est vraiment pas les calculs qui sont long.
On cheche donc tout lestels que
,
et
.
(1) Sion doit avoir
et
:
(2) Sion doit avoir
et
:
Merci pour toutes tes précisions Ben ca m'aide beaucoup
ok je vais continuer à bosser cela
la par exemple en exam aujourd'hui j'ai eu:
déterminer les polynômes irréductibles de degré 2 et 3 dans F2
j'en ai trouvé un de degré 2 et deux de degré 3
puis la questions suivantes:
en déduire que X^6 + X +1 est irréductible sur F2
et là je n'ai pas su quoi dire
Re: Polynômes irréductibles Z/pZ[X]
Si X^6 + X + 1 était réductible, on pourrait l'écrire comme produit de polynômes de degrés inférieurs. J'ai testé les produits suivants (bien entendu tout est dans Z/2Z[X]):
(x^3 + x + 1)^2 = x^6 + x^2 + 1
(x^3 + x^2 + 1)^2 = x^6 + x^4 + 1
(x^2 + x + 1)^3 = x^6 + x^5 + x^3 + x + 1
(x^3 + x + 1)(x^3 + x^2 + 1) = 1 + x^2 + x^3 + x^4 + x^5 + x^6
Mais cela me parait insuffisant vu qu'il faut aussi voir les degrés 4 (irréductibles!) par exemple et faire des produits avec des degrés 2 pour tester...Il doit y avoir autrement.
(x^3 + x + 1)^2 = x^6 + x^2 + 1
(x^3 + x^2 + 1)^2 = x^6 + x^4 + 1
(x^2 + x + 1)^3 = x^6 + x^5 + x^3 + x + 1
(x^3 + x + 1)(x^3 + x^2 + 1) = 1 + x^2 + x^3 + x^4 + x^5 + x^6
Mais cela me parait insuffisant vu qu'il faut aussi voir les degrés 4 (irréductibles!) par exemple et faire des produits avec des degrés 2 pour tester...Il doit y avoir autrement.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Polynômes irréductibles Z/pZ[X]
Lostounet a écrit:Si X^6 + X + 1 était réductible, on pourrait l'écrire comme produit de polynômes de degrés inférieurs. J'ai testé les produits suivants (bien entendu tout est dans Z/2Z[X]):
(x^3 + x + 1)^2 = x^6 + x^2 + 1
(x^3 + x^2 + 1)^2 = x^6 + x^4 + 1
(x^2 + x + 1)^3 = x^6 + x^5 + x^3 + x + 1
(x^3 + x + 1)(x^3 + x^2 + 1) = 1 + x^2 + x^3 + x^4 + x^5 + x^6
Mais cela me parait insuffisant vu qu'il faut aussi voir les degrés 4 (irréductibles!) par exemple et faire des produits avec des degrés 2 pour tester...Il doit y avoir autrement.
Salut Loustounet merci pour ta réponse,
en effet cela est insuffisant, de plus je me vois mal en exam donc en temps limité, devoir tester toutes les combinaisons possibles et imaginables...
Soit il y a une astuce qui nous a échappé au premier coup d oeil soit la question nécessite du temps pour essayer de déduire la réponse d'une masse de procédés purement calculatoires et alors je ne vois le but de faire cela en examen...
Re: Polynômes irréductibles Z/pZ[X]
Un polynôme de degré 2 est irréductible ssi il est sans racines donc c'est lesyoshi13 a écrit:déterminer les polynômes irréductibles de degré 2 dans F2
Il y en a donc un seul :
Idem pour le degré 3 : c'est lesyoshi13 a écrit:déterminer les polynômes irréductibles de degré 3 dans F2
Il y en a donc deux :
(1) Commeyoshi13 a écrit:en déduire queest irréductible sur F2
(2)
(3)
Et c'est fini vu que s'il était factorisable un des facteurs au moins devrait être de degré inférieur ou égal à 3.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynômes irréductibles Z/pZ[X]
Rebonjour
Puisque le sujet à l'air d'intéresser, voici un exemple que j'aime bien. Le polynôme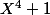 est réductible dans tous les corps finis!
est réductible dans tous les corps finis!
Puisque le sujet à l'air d'intéresser, voici un exemple que j'aime bien. Le polynôme
Re: Polynômes irréductibles Z/pZ[X]
Ben314 a écrit:Un polynôme de degré 2 est irréductible ssi il est sans racines donc c'est lesyoshi13 a écrit:déterminer les polynômes irréductibles de degré 2 dans F2tel que
(dans F2,
équivaut à
) et
.
Il y en a donc un seul :Idem pour le degré 3 : c'est lesyoshi13 a écrit:déterminer les polynômes irréductibles de degré 3 dans F2tel que
et
.
Il y en a donc deux :et
(1) Commeyoshi13 a écrit:en déduire queest irréductible sur F2
le polynôme
n'a pas de facteur de degré 1.
(2)donc
n'est pas divisible par
et cela prouve que
n'admet pas de facteur irréductible de degré 2.
(3)et
donc
n'est divisible ni par
, ni par
et donc n'admet aucun facteur irréductible de degré 3.
Et c'est fini vu que s'il était factorisable un des facteurs au moins devrait être de degré inférieur ou égal à 3.
Merci pour tous ces détails Ben, je vais regarder ça tranquillement, si jamais j'ai des questions je reviens t'embêter
Re: Polynômes irréductibles Z/pZ[X]
Mimosa a écrit:Rebonjour
Puisque le sujet à l'air d'intéresser, voici un exemple que j'aime bien. Le polynômeest réductible dans tous les corps finis!
Merci Mimosa, c'est bon à savoir
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
