Polynomes Decomposition en facteurs irréductibles
17 messages
- Page 1 sur 1
Polynomes Decomposition en facteurs irréductibles
Bonjour à tous,
je travaille avec des polynômes à coefficients dans Z/NZ, N composé.
Soit donc P \in Z/NZ[X] de degré p, (pour pouvoir avoir une division euclidienne, je prends des polynômes qui ont un coefficient dominant inversible, voire des polynômes unitaires pour simplifier...)
Z/NZ[X] est Noetherien mais pas intègre, il existe donc DES décompositions en facteurs irréductibles de P.
Je souhaiterais obtenir une majoration du nombre de facteurs irréductibles "différents" (qui ne sont pas égaux modulo multiplication par un inversible) qui peuvent intervenir dans ces décompositions, toutes confondues.
Quelqu'un ici connaîtrait il un résultat qui pourrait me mettre sur la voie..?
ps: La documentation sur les polynômes à coefficients dans un anneau quelconque (surtout pas intègre) étant assez rare, ce serait vraiment bien si vous aviez déjà quelques références...
Merci à tous et bon week end
je travaille avec des polynômes à coefficients dans Z/NZ, N composé.
Soit donc P \in Z/NZ[X] de degré p, (pour pouvoir avoir une division euclidienne, je prends des polynômes qui ont un coefficient dominant inversible, voire des polynômes unitaires pour simplifier...)
Z/NZ[X] est Noetherien mais pas intègre, il existe donc DES décompositions en facteurs irréductibles de P.
Je souhaiterais obtenir une majoration du nombre de facteurs irréductibles "différents" (qui ne sont pas égaux modulo multiplication par un inversible) qui peuvent intervenir dans ces décompositions, toutes confondues.
Quelqu'un ici connaîtrait il un résultat qui pourrait me mettre sur la voie..?
ps: La documentation sur les polynômes à coefficients dans un anneau quelconque (surtout pas intègre) étant assez rare, ce serait vraiment bien si vous aviez déjà quelques références...
Merci à tous et bon week end
Sumeera a écrit:Soit donc P \in Z/NZ[X] de degré p, (pour pouvoir avoir une division euclidienne, je prends des polynômes qui ont un coefficient dominant inversible, voire des polynômes unitaires pour simplifier...)
Tu prends P unitaire? ou bien tu limites la recherche aux "diviseurs" de P qui sont unitaires?
Dans le premier cas, je ne vois pas pourquoi on aurait un nombre fini de diviseurs de P : tu n'as pas de limitation des degrés de ces diviseurs.
yos a écrit:Tu prends P unitaire? ou bien tu limites la recherche aux "diviseurs" de P qui sont unitaires?
Dans le premier cas, je ne vois pas pourquoi on aurait un nombre fini de diviseurs de P : tu n'as pas de limitation des degrés de ces diviseurs.
Bonjour Yos,
En fait, il faut que P et ses "diviseurs" aient leurs coefficients dominants inversibles modulo N, et je considère également que 2 polynômes de Z/NZ[X] sont équivalents s'ils sont égaux modulo multiplication par un inversible, donc il me semble que cela me permet de ne considérer que les polynômes unitaires (pour P et ses "diviseurs")...
Donc je pense que les "diviseurs" de P seraient alors de degré < à degré de P
Par contre, ThSQ, (bonjour)
ThSQ a écrit:Problème intéressant. Tu veux une majoration avec quelle "finesse" (c'est facile de majorer le nombre de polynômes unitaires qui divise un polynôme donné) ?
je ne sais pas vraiment quelle "finesse" je recherche, c juste que je ne vois pas pour l'instant comment majorer ce nombre de diviseurs autrement que "brutalement" par le nombre de polynomes irréductibles de degré inférieur à degré de P...
Si tu as une autre majoration, je suis intéressée..! :happy2:
Merci
[quote="Sumeera"]
Donc je pense que les "diviseurs" de P seraient alors de degré à degré de P, alors son coefficient dominant est un diviseur de zéro " mais après y avoir regardé d'un peu plus près, ça me semble faux maintenant...
Désolée...
Du coup Yos, je crains maintenant que tu aies raison ..! Et que n'ayant pas de limite sur le degré, je ne puisse pas trouver la majoration que je souhaite...
Bon we
Donc je pense que les "diviseurs" de P seraient alors de degré à degré de P, alors son coefficient dominant est un diviseur de zéro " mais après y avoir regardé d'un peu plus près, ça me semble faux maintenant...
Désolée...
Du coup Yos, je crains maintenant que tu aies raison ..! Et que n'ayant pas de limite sur le degré, je ne puisse pas trouver la majoration que je souhaite...
Bon we
La situation n'est pas simple modulo n.
Pour un polynôme unitaire, a-t-on existence d'une factorisation en irréductibles unitaires ? la réponse est non :
Factoriser un polynôme unitaire peut se faire avec des polynômes irréductibles pas "monic" (unitaire à un facteur inversible près), et de même degré : par exemple, dans Z/6Z[x], on a (4x+1)(3x+1)=x+1
Et aucun des polynômes x+... ne divise x+1 (mis à part x+1, qui n'est pas irréductible)
Il faudrait déjà regarder sur Z/p^nZ avec p premier. Dans ce cadre-là, il y a "juste" un problème de nilpotence. Mais c'est déjà pas mal !
Pour un polynôme unitaire, a-t-on existence d'une factorisation en irréductibles unitaires ? la réponse est non :
Factoriser un polynôme unitaire peut se faire avec des polynômes irréductibles pas "monic" (unitaire à un facteur inversible près), et de même degré : par exemple, dans Z/6Z[x], on a (4x+1)(3x+1)=x+1
Et aucun des polynômes x+... ne divise x+1 (mis à part x+1, qui n'est pas irréductible)
Il faudrait déjà regarder sur Z/p^nZ avec p premier. Dans ce cadre-là, il y a "juste" un problème de nilpotence. Mais c'est déjà pas mal !
Sumeera a écrit:Je crois que j'ai dit une bêtise... Je pressentais un truc du style: "si un diviseur de P a un degré > à degré de P, alors son coefficient dominant est un diviseur de zéro " mais après y avoir regardé d'un peu plus près, ça me semble faux maintenant...
Si ça doit marcher. Suppose P=QR avec Q et R unitaires :
Ca marche même avec seulement Q unitaire.
Du coup la majoration par le nombre de polynômes irréductibles de degré au plus n est valable. Cela dit ce dernier nombre est encore un mystère. Allons-y plus franchement en majorant par le nombre de polynômes de degré au plus n.
Mieux je vois pas.
leon1789 a écrit:Pour un polynôme unitaire, a-t-on existence d'une factorisation en irréductibles unitaires ? la réponse est non :
Factoriser un polynôme unitaire peut se faire avec des polynômes irréductibles pas "monic" (unitaire à un facteur inversible près), et de même degré : par exemple, dans Z/6Z[x], on a (4x+1)(3x+1)=x+1
D'où ma question dans mon premier message. Mais ici on suppose que les diviseurs sont unitaires. D'où la formule des degrés deg(PQ)=...
Pour le reste, je ne songeais pas à utiliser des propriétés d'anneau factoriel.
yos a écrit:D'où ma question dans mon premier message. Mais ici on suppose que les diviseurs sont unitaires. D'où la formule des degrés deg(PQ)=...
Pour le reste, je ne songeais pas à utiliser des propriétés d'anneau factoriel.
Donc le problème passe de "polynomes irréductibles divisant un polynome unitaire fixé", à "polynomes unitaires divisant un polynôme unitaire fixé" . OK.
Bonsoir Leon1789,
Je suis d'accord avec l'exemple que tu donnes, cependant, les polynômes que je considère sont ceux ayant un coefficient dominant inversible modulo N, et ton exemple confirme un peu mon "pressentiment" qui est que si les degrés des diviseurs sont > (ou égaux du coup!) au degré de P, alors leurs coefficients dominants sont des diviseurs de zéro ( 3 et 4 mod 6)...
De par mes hypothèses, je "redéfinis" (sans prétention) la notion de factorisabilité, qui deviendrait P est factorisable s'il est divisible par un polynôme irréductible unitaire.
Cependant le problème reste complet, puisque pour rester dans Z/6Z[x], le polynôme x^2 + x par exemple admet plusieurs décompositions en facteurs unitaires, à savoir x(x+1) et (x+3)(x+4)...
Peut-on alors quand même majorer le nombre de polynômes unitaires divisant un polynôme donné..?
Je suis d'accord avec l'exemple que tu donnes, cependant, les polynômes que je considère sont ceux ayant un coefficient dominant inversible modulo N, et ton exemple confirme un peu mon "pressentiment" qui est que si les degrés des diviseurs sont > (ou égaux du coup!) au degré de P, alors leurs coefficients dominants sont des diviseurs de zéro ( 3 et 4 mod 6)...
De par mes hypothèses, je "redéfinis" (sans prétention) la notion de factorisabilité, qui deviendrait P est factorisable s'il est divisible par un polynôme irréductible unitaire.
Cependant le problème reste complet, puisque pour rester dans Z/6Z[x], le polynôme x^2 + x par exemple admet plusieurs décompositions en facteurs unitaires, à savoir x(x+1) et (x+3)(x+4)...
Peut-on alors quand même majorer le nombre de polynômes unitaires divisant un polynôme donné..?
Je reviens sur 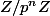
Tout diviseur unitaire de P (unitaire aussi) passe modulo p . Là, dans Z/pZ (corps), on sait qu'un polynôme P de degré d ne peut avoir qu'un nombre maximum de diviseurs, majoré par une fonction de d.
On imagine maintenant remonter les diviseurs de Z/pZ[X] dans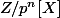 . En général, ce n'est pas possible, mais on fait comme si (puisqu'on veut seulement un majorant du nombre de diviseurs).
. En général, ce n'est pas possible, mais on fait comme si (puisqu'on veut seulement un majorant du nombre de diviseurs).
Pour cela, on peut utiliser le nombre d'éléments dans Ker de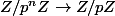 qui est
qui est 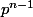 ...
...
Tout diviseur unitaire de P (unitaire aussi) passe modulo p . Là, dans Z/pZ (corps), on sait qu'un polynôme P de degré d ne peut avoir qu'un nombre maximum de diviseurs, majoré par une fonction de d.
On imagine maintenant remonter les diviseurs de Z/pZ[X] dans
Pour cela, on peut utiliser le nombre d'éléments dans Ker de
Je me suis aperçue que vous aviez posté pdt que je rédigeais mon dernier message...
Je me permets de repréciser un peu pourquoi je ne regarde que les diviseurs unitaires, puisqu'il semble que ce soit un peu litigieux...
en fait c'est justement pour pouvoir parler de division que je ne prends que les polynômes à coeff dominant inversible, et avec la relation d'équivalence P~Q si Q=aP a inversible mod N, je peux ne regarder que les diviseurs unitaires...
Parce que si le coeff dominant du "diviseur" est un diviseur de zéro, on ne peut pas avoir de division euclidienne de P par son "diviseur", ce que je trouve plutôt gênant...
Je me permets de repréciser un peu pourquoi je ne regarde que les diviseurs unitaires, puisqu'il semble que ce soit un peu litigieux...
leon1789 a écrit:Donc le problème passe de "polynomes irréductibles divisant un polynome unitaire fixé", à "polynomes unitaires divisant un polynôme unitaire fixé" . OK.
en fait c'est justement pour pouvoir parler de division que je ne prends que les polynômes à coeff dominant inversible, et avec la relation d'équivalence P~Q si Q=aP a inversible mod N, je peux ne regarder que les diviseurs unitaires...
Parce que si le coeff dominant du "diviseur" est un diviseur de zéro, on ne peut pas avoir de division euclidienne de P par son "diviseur", ce que je trouve plutôt gênant...
Je vous remercie de chercher avec moi une solution à ce problème un vendredi soir..!
Par contre Leon1789, je suis "obligée" de travailler avec des polynômes à coefficients dans Z/NZ, N composé...
Puis il me semble que la question avec les coefficients dans un corps fini ne se pose pas vraiment... L'anneau des polynômes à coefficients dans un corps fini est un anneau euclidien donc principal donc factoriel, donc un polynôme de degré m a au plus m facteurs irréductibles, non..?
Par contre Leon1789, je suis "obligée" de travailler avec des polynômes à coefficients dans Z/NZ, N composé...
Puis il me semble que la question avec les coefficients dans un corps fini ne se pose pas vraiment... L'anneau des polynômes à coefficients dans un corps fini est un anneau euclidien donc principal donc factoriel, donc un polynôme de degré m a au plus m facteurs irréductibles, non..?
Sumeera a écrit:Parce que si le coeff dominant du "diviseur" est un diviseur de zéro, on ne peut pas avoir de division euclidienne de P par son "diviseur", ce que je trouve plutôt gênant...
"Coef dominant de Q inversible" est une condition suffisante pour pouvoir diviser par Q mais nullement nécessaire : voir l'exemple de Leon 1815.
Sumeera a écrit:Je vous remercie de chercher avec moi une solution à ce problème un vendredi soir..!
Par contre Leon1789, je suis "obligée" de travailler avec des polynômes à coefficients dans Z/NZ, N composé...
avec le théorème chinois, on pourra passer de
Sumeera a écrit:Puis il me semble que la question avec les coefficients dans un corps fini ne se pose pas vraiment... L'anneau des polynômes à coefficients dans un corps fini est un anneau euclidien donc principal donc factoriel, donc un polynôme de degré m a au plus m facteurs irréductibles, non..?
oui, mais maintenant on veut des diviseurs unitaires (pas forcément irréductibles), c'est davantage que m.
Je pensais passer de Z/pZ à Z/p^nZ, puis Z/NZ. Mais ça donne quoi au final ???
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
