Matrice et noyau
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 14:02
par Damian29 » 13 Avr 2009, 14:02
bonjour à tous
je suis en train de faire un exo sur les matrices mais je suis pas sur que ce que j'avance est correct ou nn
voici le sujet :
Soit A=2 0 une matrice de M2(IK)
-1 3
on considere l'endomorphisme £ de M2(IK) défini par £(m)=Am-mA
déterminer les dimensions kerf(£)
pour cela je pense q'uil faut trouver d'abord ker(£) trouver une base et en déduire la dimension
si m appartient Ker(£)<==>f(m)=0<==>Am=mA
et c'est la que je suis pas sur
pour moi cette égalité est vrai uniquement si m est la matrice nul non?
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 14:17
par Damian29 » 13 Avr 2009, 14:17
alr en fait nn
sa marche également pour les matrices nuls, identité,et scalaire
ainsi une base de de ker(£)=((0),matrices identité,matrice scalaire)
si c'est cela ne peut t'on pas rassembler matrice identité et scalaire en mm tp?
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 14:59
par Damian29 » 13 Avr 2009, 14:59
pour moi je dirais que Ker(f)=vect(Im=matrice identité)
mais je suis aps sur...
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 16:31
par emdro » 13 Avr 2009, 16:31
Bonjour,
As-tu essayé de calculer £
)
, par exemple?
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 16:40
par Damian29 » 13 Avr 2009, 16:40
ba je veux bien mais £(A)=Am-mA
et m on le connait pas...
d'après toi ce que j'ai dit avant est juste ou faux pk moi je suis parti en disant que A=vect(matrice identité) car seul la matrice nul, scalaire et identité vérifie Am=mA
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 16:44
par Damian29 » 13 Avr 2009, 16:44
dzl mal écris
ker(£)=vect(matrice identité)
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 16:44
par emdro » 13 Avr 2009, 16:44
Ce n'est pas £(A)=Am-mA, mais £(m)=Am-mA.
Du coup, tu peux comme je te le suggère calculer £(M)=AM-MA, où M est la matrice que je t'ai donnée.
D'autre part, ce n'est en aucun cas: A=vect(matrice identité), mais éventuellement Ker£= vect(matrice identité).
Et tu verras en faisant le calcul que je t'ai proposé que c'est faux.
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 16:47
par Damian29 » 13 Avr 2009, 16:47
ou dzl je me suis rectifié aprés ^^'
a lol
alr quel est linterêt de me mettre sur un piste qui est fausse ^^"
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 16:51
par emdro » 13 Avr 2009, 16:51
C'est TON hypothèse qui est fausse. Pas ce que je te propose!
Fais le calcul que je t'ai suggéré.
Dis-moi si la matrice que j'ai proposée est dans Vect(Id).
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 16:57
par Damian29 » 13 Avr 2009, 16:57
ba sa fait O oO'
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 17:00
par emdro » 13 Avr 2009, 17:00
Donc
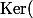
£
\neq \mathbb R \text{Id}_2)
!
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 17:05
par Damian29 » 13 Avr 2009, 17:05
dzl mais je vois pas se que sa m'apporte :/ :S :$
avec ce constat on en déduit que mon hypothèse est fausse ou nn?
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 17:13
par emdro » 13 Avr 2009, 17:13
Je ne vois pas très bien ton raisonnement:
tu commences par dire que seule m=0 donne Am-mA=0.
Ensuite, tu affirmes à l'arrache que seules les matrices scalaires (m=lambda I) vérifient Am-mA=0.
Je te donne une matrice non scalaire M telle que AM-MA=0, et tu ne vois pas la conclusion?
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 17:16
par Damian29 » 13 Avr 2009, 17:16
a oki!
sa me permet d'affirmer que seul des matrices scalaire peuvent vérifier Am=mA
dc que mon hypothèse est vrai
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 17:18
par Damian29 » 13 Avr 2009, 17:18
a nn dzl pfff je suis tp perdu... :(
en prenant A on vois que sa fais 0
dc il n'y pas que les matrices scalaire en jeu...
mon hypothes est fausse
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 17:21
par emdro » 13 Avr 2009, 17:21
Ce qui m'inquiète, c'est que tu sembles affirmer des choses comme si c'était évident. Alors que c'est faux...
Tu penses qu'on doit voir d'un coup d'oeil l'ensemble des matrices m telles que Am-mA=0?
Ce n'est pas le cas. Il faut les chercher en faisant des calculs...
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 17:25
par Damian29 » 13 Avr 2009, 17:25
il est vrai qu'au début je me suis précipité et ai vu uniquement la matrice nul
puis j'ai commencé à faire les calcules pour les autres matrices juste aprés avoir le premier mess..c'est vrai là j'ai pas réfléchi
mais j'ai pas pensé a vérifié avec A....
-
emdro
- Membre Complexe
- Messages: 2351
- Enregistré le: 11 Avr 2007, 16:37
-
 par emdro » 13 Avr 2009, 17:28
par emdro » 13 Avr 2009, 17:28
Il faut juste faire tous les calculs. C'est un peu pénible, mais pas difficile.
Lorsque tu auras trouvé la réponse, donne-la moi. Je te dirai si c'est ça :happy2:
-
Damian29
- Membre Relatif
- Messages: 172
- Enregistré le: 01 Nov 2008, 12:35
-
 par Damian29 » 13 Avr 2009, 17:31
par Damian29 » 13 Avr 2009, 17:31
je te remercie de ta patience :) c'est sympa et sa motive ^^
je file les faire :)
-
Le Chaton
- Membre Irrationnel
- Messages: 1335
- Enregistré le: 12 Oct 2008, 19:00
-
 par Le Chaton » 13 Avr 2009, 18:03
par Le Chaton » 13 Avr 2009, 18:03
Bonjour,
pourquoi ne pas appelé
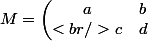
Ensuite tu détermines les valeurs pour lesquelles AM=MA ... ( donc tu calcules AM et MA )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
