Exercices espaces vectoriels

[Ben314]

Le a) et le b) sont "complètement cons" i.e. il suffit de connaitre la définition du produit d'une matrice par un vecteur.
Si tu donne des noms aux vecteurs colonnes de A : V_1,V_2 ... V_? (combien y en a-t-il ?) et que tu écrit X=(x_1 x_2 ... x_?) EN COLONNE (quand on tape du texte, c'est super chiant de les écrire en colonne, mais, normalement, les éléments de R^? sont des vecteurs colonnes) alors, comment peut on écrire AX ?

P.S. La définition du noyau t'est donné au début de l'énoncé...

[jklmmlkj]

Oui, c'est ce que j'ai fait, (V_1, V_2, ... V_n)(x_1, x_2, ... x_n) en colonne et donc on a une matrice m x 1.

[Ben314]

Ici, regarde bien la définition du produit de deux matrices (ou du produit matrice/vecteur) pour voir que le résultat est... trés simple.

[jklmmlkj]

Eh ben comme on a une matrice (m x n)*(n x 1), on aura bien une matrice B (m x 1) = (VI*x1, V2*x2, ... ,Vn*xn) (en ligne).

[Ben314]

Eh ben comme on a une matrice (m x n)*(n x 1), on aura bien une matrice B (m x 1) = (VI*x1, V2*x2, ... ,Vn*xn) (en ligne).

Oui, on aurra bien comme résultat une matrice mx1 mais...
la matrice que tu donne comme résultat n'est pas mx1 mais mxn !!!
essaye de prendre A de taille 3x2 avec dedans a b c... et X=(x_1 x_2).
Fait ton produit et essaye de voir le lien avec les deux vecteurs colonnes de A...

[jklmmlkj]

Ok, merci.

Donc == sauf que c'est une matrice 3x1 puisque V1 appartient a R^3.

Du coup, je peux directement dire que AX appartient à R^m si le nombre de ligne de la matrice A est m?

[Ben314]

Oui, c'est ca.
Le fait que AX soit dans R^m n'est pas vraiment trés nouveau comme information (ca risque d'étre dans la définition du produit....)
Ce qui est plus important, c'est que DANS TON CAS PARTICULIER, tu as trés bien vu que AX=x_1V_1+x_2V_2 (quand tu fait un produit vecteur x réel, prend l'habitude de mettre le réel en premier)
Dans le 1) il faut faire un vague discours (je saurais pas trop quoi mettre...) pour expliquer que cette formule est tout le temps vraie....
Je proposerais bien un truc du style :
"En utilisant la définition du produit de deux matrices, il est clair que...."
Ou alors tu écrit la même chose que dans l'exemple mais avec des a_1,1 a_1_2... et des points de suspension.
Oui, c'est sans doute plus propre avec les a_1,1... (mais c'est chiant à écrire) : essaye de le faire (il suffit de "copier" le cas particulier en mettant des (doubles) indices et des points de suspension)

P.S. En plus, si tu veux que je vérifie, c'est encore plus gonflant à écrire en TeX qu'a la main...

[jklmmlkj]

Ok, merci! Et pour le b, c'est le même principe non?

Et pour la c), est ce que Im() = X ou .

Parce que sinon j'ai fais
KerA Im()
AX=0 X
X 0

Puis on cherche v tel que v = X = 0.

[Ben314]

Pour le b), c'est "à peu prés" la même chose.
Pour le c) im(tA) est (évidement) l'ensemble de tA.Y avec Y un vecteur colonne de R^m (donc il vaut mieux ne pas l'appeler X qui lui, était dans R^n) tu peut si tu veux dire que c'est l'ensemble des tA.tY' avec Y un vecteur ligne de taille m, ca ne change rien (et c'est sans intérêt)

[jklmmlkj]

D'accord merci beaucoup, finalement le c) n'est pas compliqué, le d) par contre il faut voir la démonstration du théorème du rang je pense.

[Ben314]

Pour le d) il suffit de regarder en terme de dimension ce que tu as démontré.
On cherche à te faire démontrer le théorème du rang donc, normalement, il est interdit de s'en servir dans l'exo...

[jklmmlkj]

Avec la question c) je trouve que Im() = mais est ce qu'on peut savoir grâce à ca que dim() = n? Et il s'agit bien de démontrer en plus que dim(KerA) = 0?
Merci.

[Ben314]

S'il était vrai que Im(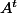) = , tu pourrait en déduire que dim(Im(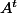)) = dim()=n. (on ne peut pas écrire dim(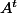) car 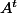est une matrice, pas un s.e.v.)
Sauf que ce n'est pas (forcémént) vrai.
Dans le c) rien ne dit que le Im est R^n et le Ker est {0} : on sait simplement que les deux sont suplémentaires....

[jklmmlkj]

Ok, ben ils se sont trompés dans l'exo alors parce qu'il est écrit "en admettant que dim() = dim(ImA), c'est plutôt dim(Im) = dim(ImA) non ?

Et dans le c) comme ils sont supplémentaires, cela veut bien dire que KerA + Im() = mais comme KerA = AX = 0, alors Im() = ?

Merci.

[Ben314]

Oui, tu as raison pour le dim(tA) (j'avais encore pas super bien lu l'énoncé....)
Pa contre "KerA = AX = 0" ne vas pas du tout : Ker(A) est un s.e.v. c'est à dire un ensemble de vecteurs alors que AX et 0 sont des vecteurs (et en plus je ne vois pas qui serait X ici)
Ce qui pourrait avoir un sens ce serait par exemple Ker(A)={0} (ca aurait un sens mais ca serait faux !!!!)
Ici, Ker(A) est l'ensemble des vecteurs X tels que AX=0.
Il peut être trés gros : Si la matrice A ne contient que des 0 alors tout les vecteurs X vérifient AX=0 donc, dans ce cas particulier on a Ker(A)=R^n.

[jklmmlkj]

Ah ok merci, je n'avais pas compris comme ca, donc du coup, mon c) est tout faux. Et donc c'est quoi qui est juste dans le d) dim() = dim(ImA) ou dim(Im) = dim(ImA)?

[Ben314]

C'est dim(Im) = dim(ImA)
(l'autre ne veut rien dire)

[jklmmlkj]

D'accord, merci.

[houda 20]

salut
désolé pour le retard. mais vraiment pas de temps
ton exo ne parait pas trop difficile. il demande juste un peu de reflexion
pour le 1)
pour démontrer que c'est un sev c'est évident je pense

on a AX= a11*x1+a12*x2+........+a1n*xn




am1*x1+am2*x2+.......+amn*xn

c'est un vecteur de m ligne et d'une seule colonne
de cette écriture tu peux tirer les deux premières questions

a suivre

[houda 20]

le vecteur ci dessus n'est pas bien écrit
regarde
A*X= la première composante




la dernière composante