Exercices espaces vectoriels

[houda 20]

tu sais. j'aimais toujours travaillé avec ses choses là des dimensions. ca raccourci trop le chemin quand il ne s'agit pas des calculs.
pour le 5)
je ne vais pas calculer aussi
dis moi; EST CE QUE VOUS AVEZ trouvé que leur intersection vaut {0}

[Ben314]

Fait attention Houda20, pour être sur que la dimension du deuxième est 3, il faudrait savoir si la famille dans le "vect" est libre, or, justement, la formule que vient de trouver jklmmlkj montre que la famille n'est pas libre
donc la dimension de vect{e_1,e_2,e_3} est strictement plus petite que 2.

Pour trouver quelle dimension c'est, il faut voir que la formule de jklmmlkj peut s'écrire sous la forme :
un des 3 = une combinaison linéaire des 2 autres
et cela signifie que celui qui s'écrit en fonction des deux autres ne sert à rien dans le vect. -> on peut l'enlever.

Maintenant, on peut, soit avec des arguments de dimension (comme le suggére Houda20), soit "à la main" finir ce 5)....

[jklmmlkj]

Oui, on a trouvé que l'intersection vaut {0} pour le 5. Sinon, j'avoue que je ne suis pas très a l'aise avec les dimensions du fait que j'ai appris ca il n'y a pas longtemps et que je ne maîtrise pas tous encore.

[houda 20]

Fait attention Houda20, pour être sur que la dimension du deuxième est 3, il faudrait savoir si la famille dans le "vect" est libre, or, justement, la formule que vient de trouver jklmmlkj montre que la famille n'est pas libre
donc la dimension de vect{e_1,e_2,e_3} est strictement plus petite que 2.

Pour trouver quelle dimension c'est, il faut voir que la formule de jklmmlkj peut s'écrire sous la forme :
un des 3 = une combinaison linéaire des 2 autres
et cela signifie que celui qui s'écrit en fonction des deux autres ne sert à rien dans le vect. -> on peut l'enlever.

Maintenant, on peut, soit avec des arguments de dimension (comme le suggére Houda20), soit "à la main" finir ce 5)....

non ben314. j'ai bien vérifié les calculs
regarde. on le calcule de cette facon
a*(0,1,-2,1)+b*(1,0,2,-1)=c*(1,0,2,-1)+d*(3,2,2,-1)+e*(0,0,1,0)=x

on résout le système pour chercher les coefficients a,b;c,d,e
on trouve à la fin
a=2d
b=c+3d
e=0

vérifie les calculs et dis moi. normalement tu retombes sur le meme résultat

donc

x=c*(1,0,2,-1)+d*(3,2,2,-1)

tu trouveras ca dans les deux cotés en remplacant chacun avec sa valeur trouvée en fonction de c et d "moi j'ai choisi c et d. on peut choisir d'autres"

[Ben314]

A ce moment là essaye de commencer par montrer plus ou moins à la main le dernier résultat qui manque.
Puis, si tu n'en a pas complètement marre, essaye de voir comment on aurait pu raisonner avec les dimensions (je vient seulement de me rendre compte que certaines questions étaient liées entre elles... en utilisant les dimension tu aurais donc gagné du temps...)

P.S. Tu as raison HOULA20, je me suis emmélé les pinceaux entre les différents exercices et je croyais que tu parlais du 5)...

[houda 20]

Oui, on a trouvé que l'intersection vaut {0} pour le 5. Sinon, j'avoue que je ne suis pas très a l'aise avec les dimensions du fait que j'ai appris ca il n'y a pas longtemps et que je ne maîtrise pas tous encore.

oui. c'est un peu difficile au début

mais crois moi. en faisant une bonne quantité d'exos. tu pourras t'en sortir merveilleusement.

il faut que tu les maitrises. les calculs ne sont pas toujrs guarantis. tu risques tjrs de faire des fautes qui te couteront des notes bien précieuse

rien n'est difficile avec le travail sérieux. ok!!!!!!!!

[Ben314]

Je rajouterais, ce qui vas tout à fait dans le sens de HOULA20, que les arguments de dimension permettent (au minimum) de faire deux fois moins de calculs....
Mais il faut aussi comprendre quel sont les calculs qui deviennent inutile et, pour cela, je pense qu'il faut les avoir fait au moins une fois ou 2.

[jklmmlkj]

C'est ce chapitre qui est dur, et c'est mal expliqué dans mon cours... Et j'ai encore un autre exo après celui la qui est encore plus dur... Par contre, maintenant que j'ai mis au propre les propositions 1, 2, 3, et 4, je ne pense pas que je vais recommencer avec les dimensions...

[houda 20]

le 5) est vrai
car dim de la somme=4
car e3 est une combinaison linéaire de e1 et e2 et don la dim de Vect{e_1,e_2,e_3} est 2
on a 2+2-0"la dim de{0]"=4
et puisque Vect{e_4,e_5} +Vect{e_1,e_2,e_3} est un sev de R^4 de dim 4 alors il est bien égal à R^4

dis moi. tu as fais cette proposition
si F est un sev de E et dim E=dimF alors E=F

elle est vraie cette proposition n'est ce pas?? j'ai un trouble de mémoire terrible...... :help: :help: :help:

si elle est vrai. voila ton exo.........ouf enfin

[jklmmlkj]

J'ai vu cette proposition qu'hier matin : si F est un sev de E de dim E = n et si dim F = n alors F=E.

[houda 20]

C'est ce chapitre qui est dur, et c'est mal expliqué dans mon cours... Et j'ai encore un autre exo après celui la qui est encore plus dur... Par contre, maintenant que j'ai mis au propre les propositions 1, 2, 3, et 4, je ne pense pas que je vais recommencer avec les dimensions...

mais pourquoi tu ne te références pas aux livres?????????
il faut que tu résous une bonne quantités d'exos pour pouvoir bien les manipuler. bon je penses que ton problème n'est pas la mal compréhension du cours mais c'est que tu ne sais pas comment utiliser tes propositions et tes théorèmes. c'est ca ce qui est le plus difficile en math. c'est avoir du bon raisonnement. et le bon raisonnement ne viens pas que si on bosse beaucoup.

maintenant je pense que tu dois refaire le 4). eh,tu ne m'as pas dis comment vous avez fait..........
il n y a que le 4 ou on a utilisé la dim

[houda 20]

J'ai vu cette proposition qu'hier matin : si F est un sev de E de dim E = n et si dim F = n alors F=E.

alors..........c'est fini. on l'a eu cet exo :we: :we: :we: :we: :we: :we:

[houda 20]

le 4 est bien faux non??????

[jklmmlkj]

Ben pour le 4, j'ai fait Vect{e_1,e_2} + Vect{e_2, e_3, e_4} = vect{e_1, e_2, e_3, e_4} et j'ai vérifié si la matrice composé de e_1, e_2, e_3, e_4 était inversible.
Oui j'ai trouvé que le 4 est faux.

[jklmmlkj]

Merci!! Oui, enfin fini cet exo! Mais j'en ai un dernier :(

[houda 20]

Ben pour le 4, j'ai fait Vect{e_1,e_2} + Vect{e_2, e_3, e_4} = vect{e_1, e_2, e_3, e_4} et j'ai vérifié si la matrice composé de e_1, e_2, e_3, e_4 était inversible.
Oui j'ai trouvé que le 4 est faux.

bon. je vais mentir si je dirai que j'ai compris pourquoi vous avez fait comme ca

[houda 20]

Merci!! Oui, enfin fini cet exo! Mais j'en ai un dernier

mais ce n'est pas grave
toujours la pour t'aider

[houda 20]

c'est bon c'est bon j'ai compris
en attente de l'autre exo................

[jklmmlkj]

Ok, merci beaucoup!
Voici l'énoncé :S

"Soit A une matrice réelle de forme m x n fixé. L'image de A est défini par ImA :={AX; } et le noyau de A est défini par KerA := {; AX=0}.

a. Montrer que ImA est un sev de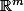 et qu'il est engendré par les vecteurs colonnes de A.

b. Montrer que KerA est sev de , constitué des vecteurs orthogonaux aux vecteurs lignes de A.

c. Montrer que = KerA + Im(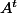) (ou "+" = somme directe et t=transposée).

d. En admettant que dim(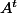) (c'est le rang de A), montrer que n = dimKerA+dimImA (théorème du rang).

e. Supposons que m=n. Si AX différent de 0 => A²X différent de 0, montrer que ImA KerA = {0}. L'inverse est vrai aussi.

f. Supposons qu m=n. Montrer que =ImA + KerA (ou "+" = somme directe) si et seulement si ImA² = ImA."

La, c'est vraiment dur , je ne sais même pas ce qu'est un noyau...

[jklmmlkj]

Pour la a), on peut écrire que AX s'écrit sous la forme et après il faut dire que ca appartient à ?
Merci.