ou bien vous pouvez suivre les étapes
l'équation de la parabole cherchée est sous la forme y-y0=a(x-x0)^2
où S(x0 ; y0) = (3;4) est le sommet et le point A(5;14) vérifie cette équation
14-4=a(5-3)^2
a=5/2
donc y-4=5/2 (x-3)^2
f(x)=5/2 (x-3)^2+4
44 résultats trouvés
Revenir à la recherche avancée
- 23 Fév 2014, 02:05
- Forum: ✎✎ Lycée
- Sujet: Exercice de maths
- Réponses: 5
- Vues: 491
- 21 Fév 2014, 13:35
- Forum: ✎✎ Lycée
- Sujet: Exercice de maths
- Réponses: 5
- Vues: 491
Bonjour à tous
Pour la fonction f; x²-1>=0 signifie que |x|>=1
Pour la fonction g; 1-x²>=0 signifie que |x|<=1
donc 1<=|x|<=1 signifie que |x|=1
D={-1;1}
Pour la fonction f; x²-1>=0 signifie que |x|>=1
Pour la fonction g; 1-x²>=0 signifie que |x|<=1
donc 1<=|x|<=1 signifie que |x|=1
D={-1;1}
- 27 Juil 2012, 16:14
- Forum: ✎✎ Lycée
- Sujet: ensemble de définition
- Réponses: 28
- Vues: 1311
Bonjour tout le monde
On utilise la formule cos²x=(1+cos 2x)/2
On cherche les racines de léquation z^7=-1
La somme de ses racines soit nulle, puis complétez
On utilise la formule cos²x=(1+cos 2x)/2
On cherche les racines de léquation z^7=-1
La somme de ses racines soit nulle, puis complétez
- 14 Juil 2012, 20:06
- Forum: ✎✎ Lycée
- Sujet: trigonométrie et nombres complexes
- Réponses: 4
- Vues: 921
La reponse de jomanaomar n'est pas satisfaisante car on utilise un cas particulier pour F et G. Les calculs de mateo49 sont bons. Si on remplace on aura:[tg^2(F)(a/b+1) + (b/a+1)]/[b+atg^2(F)] Donc si cette expression est independante de F elle vaut K. Ecrivons le et faisons le produit en croix. Pa...
- 20 Juin 2010, 04:31
- Forum: ✎✎ Lycée
- Sujet: Trigonomètrie
- Réponses: 5
- Vues: 732
luggi a écrit:Merci beaucoup!
Une dernière question encore: est-ce que quelqu'un pourrait me renvoyer à une preuve de la formule d'addtion de deux cosinus utilisée ici?

- 12 Juin 2010, 21:50
- Forum: ✎✎ Lycée
- Sujet: 2cos(2pi/5) + 2cos(4pi/5) = -1
- Réponses: 5
- Vues: 1615
Tout d'abord bonjour à tout le monde, je suis fraichement inscrit. Je cherche à prouver l'égalité suivante: 2cos(2pi/5) + 2cos(4pi/5) = -1 Après un grand nombre d'essais, je n'y parvient toujours pas... Merci en avance pour votre aide! http://www.mathmontada.net/vb/uploaded/409_1276373786.png
- 12 Juin 2010, 20:37
- Forum: ✎✎ Lycée
- Sujet: 2cos(2pi/5) + 2cos(4pi/5) = -1
- Réponses: 5
- Vues: 1615
Tout d'abord bonjour à tout le monde, je suis fraichement inscrit. Je cherche à prouver l'égalité suivante: 2cos(2pi/5) + 2cos(4pi/5) = -1 Après un grand nombre d'essais, je n'y parvient toujours pas... Merci en avance pour votre aide! http://www.mathmontada.net/vb/uploaded/409_1276373786.png
- 12 Juin 2010, 20:31
- Forum: ✎✎ Lycée
- Sujet: 2cos(2pi/5) + 2cos(4pi/5) = -1
- Réponses: 5
- Vues: 1615
Bonsoir. Dommage que l'on demande la comparaison. Ca fonctionne bien avec la règle de d'Alembert. A propos, quel type de comparaison (intégrale, majoration, équivalent)? Sinon, pour les équivalents, il y a la formule de Stirling qui donne un équivalent de n! en + \infty . comparaison avec une autre...
- 17 Fév 2009, 20:50
- Forum: ✯✎ Supérieur
- Sujet: convergence de suites
- Réponses: 9
- Vues: 959
convergence de suites
Bonsoir tout le monde,
Je n'arrive pas à résoudre ce problème
Étudier la convergence ou la divergence de la suite (somme n!/(n^n)) pour n=1 à l'infini en utilisant la comparaison.
Merci d'avance
Je n'arrive pas à résoudre ce problème
Étudier la convergence ou la divergence de la suite (somme n!/(n^n)) pour n=1 à l'infini en utilisant la comparaison.
Merci d'avance
- 17 Fév 2009, 20:16
- Forum: ✯✎ Supérieur
- Sujet: convergence de suites
- Réponses: 9
- Vues: 959
Bonjour tout le monde. M(x ; y) a pour image M'(x' ; y') Soit x' + iy' = 2x + 2iy + 3 - 4i Les points invariants existent Si x = x' et y = y' donc x = .... et y = .... Soit P(...; ...) est le point invariant Tu peux calculer les vecteurs PM' et PM et cherche la relation entre eux donc la nature de c...
- 01 Jan 2009, 23:09
- Forum: ✎✎ Lycée
- Sujet: Exercice que je n'arrive pas à faire, plutôt court, nombre complexe
- Réponses: 1
- Vues: 964
- 26 Oct 2008, 14:33
- Forum: ✎✎ Lycée
- Sujet: Devoir Maison geometrie
- Réponses: 7
- Vues: 771
Bonjour tout le monde
On peut ecrire sous la forme
sous la forme 
comme n est impaire, alors est divisible par (x + 1)
est divisible par (x + 1)
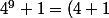(...............)) puis complète
puis complète
On peut ecrire
comme n est impaire, alors
- 26 Oct 2008, 14:23
- Forum: ✎✎ Lycée
- Sujet: Nombre Premier²
- Réponses: 9
- Vues: 509
Bonsoir tout le monde
pour les autres
5,231231231231...= 5 + x = 5+
7,456231231231231...= 7,456 + 0,0005231231231231...=
pour les autres
5,231231231231...= 5 + x = 5+
7,456231231231231...= 7,456 + 0,0005231231231231...=
- 23 Oct 2008, 20:26
- Forum: ✎✎ Lycée
- Sujet: aide pour exercice
- Réponses: 5
- Vues: 1522
Bonjour


La première fraction A est plus petite que 1 et la deuxième fraction B est plus grande que 1
La première fraction A est plus petite que 1 et la deuxième fraction B est plus grande que 1
- 18 Oct 2008, 17:43
- Forum: ✎✎ Lycée
- Sujet: comparaison et division de grands nombres
- Réponses: 5
- Vues: 1024
Bonjour,
Les deux triangles DCK et DBJ sont semblables
et les deux triangles CKIet AJI sont semblables aussi
applique les conséquences de la similitude des triangles
Les deux triangles DCK et DBJ sont semblables
et les deux triangles CKIet AJI sont semblables aussi
applique les conséquences de la similitude des triangles
- 18 Oct 2008, 17:26
- Forum: ✎✎ Lycée
- Sujet: Triangle équi demonstration
- Réponses: 1
- Vues: 503
- 18 Oct 2008, 17:18
- Forum: ✎✎ Lycée
- Sujet: simplification d'une racine
- Réponses: 6
- Vues: 967
- 44 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

