Convergence de suites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jomanaomar
- Membre Naturel
- Messages: 44
- Enregistré le: 05 Juil 2008, 08:57
-
 par jomanaomar » 17 Fév 2009, 20:16
par jomanaomar » 17 Fév 2009, 20:16
Bonsoir tout le monde,
Je n'arrive pas à résoudre ce problème
Étudier la convergence ou la divergence de la suite (somme n!/(n^n)) pour n=1 à l'infini en utilisant la comparaison.
Merci d'avance
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 17 Fév 2009, 20:43
par mehdi-128 » 17 Fév 2009, 20:43
jomanaomar a écrit:Bonsoir tout le monde,
Je n'arrive pas à résoudre ce problème
Étudier la convergence ou la divergence de la suite (somme n!/(n^n)) pour n=1 à l'infini en utilisant la comparaison.
Merci d'avance
Calcul :
lim u(n+1)/u(n)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Fév 2009, 20:45
par girdav » 17 Fév 2009, 20:45
Bonsoir.
Dommage que l'on demande la comparaison. Ca fonctionne bien avec la règle de d'Alembert. A propos, quel type de comparaison (intégrale, majoration, équivalent)?
Sinon, pour les équivalents, il y a la formule de Stirling qui donne un équivalent de n! en

.
-
jomanaomar
- Membre Naturel
- Messages: 44
- Enregistré le: 05 Juil 2008, 08:57
-
 par jomanaomar » 17 Fév 2009, 20:50
par jomanaomar » 17 Fév 2009, 20:50
girdav a écrit:Bonsoir.
Dommage que l'on demande la comparaison. Ca fonctionne bien avec la règle de d'Alembert. A propos, quel type de comparaison (intégrale, majoration, équivalent)?
Sinon, pour les équivalents, il y a la formule de Stirling qui donne un équivalent de n! en

.
comparaison avec une autre suite (soit converge, soit diverge)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Fév 2009, 22:32
par girdav » 17 Fév 2009, 22:32
jomanaomar a écrit:comparaison avec une autre suite (soit converge, soit diverge)
Dans ce cas,
!}{n.n^{n-1}} \leq \frac{(n-1)^{n-1}}{n^{n-1}} = exp((n-1)ln(1-\frac{1}{n}))
Tu peux alors montrer que
ln(1-\frac{1}{n})) = 0)
d'où la convergence.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 17 Fév 2009, 22:48
par uztop » 17 Fév 2009, 22:48
Bonjour,
girdav, qu'est ce qui te permet d'affirmer que
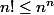
?
Je pense effectivement que Stirling est la meilleure façon de résoudre cet exo
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 18 Fév 2009, 10:03
par ThSQ » 18 Fév 2009, 10:03
Stirling c'est overkill comme on dit dans la langue de Wiles.
pour n > 1,
 \leq (n/2)^2)
et donc
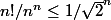
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 18 Fév 2009, 11:21
par Doraki » 18 Fév 2009, 11:21
qu'est-ce que c'est compliqué tout ça
Pour n >= 2,
n!/n^n <= 1/n * 2/n * 1 = 2/n²
La somme des 1/n² converge.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 18 Fév 2009, 11:56
par ThSQ » 18 Fév 2009, 11:56
:+++: dur de faire plus simple !
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 18 Fév 2009, 20:56
par skilveg » 18 Fév 2009, 20:56
uztop a écrit:girdav, qu'est ce qui te permet d'affirmer que
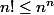
?
Par exemple
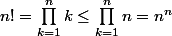
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
.
