3054 résultats trouvés
Revenir à la recherche avancée
Re: Complexité : simplifier et dominer une somme
Bonjour, on peut également majorer crûment par 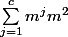 qui donne du
qui donne du ) . Ça donne une meilleure borne pour les petites valeurs de c.
. Ça donne une meilleure borne pour les petites valeurs de c.
- 09 Mar 2022, 15:22
- Forum: ✯✎ Supérieur
- Sujet: Complexité : simplifier et dominer une somme
- Réponses: 5
- Vues: 508
Re: Générateur pseudo-aléatoire d'entiers
Bonsoir, c'est pas évident deviner quel genre de réponse on attend pour la 3ème question, mais une remarque importante est que la relation de récurrence fait intervenir des petits coefficients, qui ne vont donc pas être efficaces pour "mélanger" les chiffres de X_n et produire l'illusion d...
- 17 Nov 2021, 00:16
- Forum: ✯✎ Supérieur
- Sujet: Générateur pseudo-aléatoire d'entiers
- Réponses: 9
- Vues: 658
Re: Une dérivée n ième
Comme ) tend vers 0 quand x tend vers 1, on a
tend vers 0 quand x tend vers 1, on a }-1 \sim v_n(x)\ln x \sim (x-1)v_n(x))
- 22 Aoû 2021, 23:31
- Forum: ✯✎ Supérieur
- Sujet: Une dérivée n ième
- Réponses: 11
- Vues: 800
Re: Nombre de racine d’un polynôme
Bonjour, tu as quasiment fini. Que doit satisfaire une racine multiple de Q ?
- 20 Aoû 2021, 17:42
- Forum: ✯✎ Supérieur
- Sujet: Nombre de racine d’un polynôme
- Réponses: 5
- Vues: 577
Re: Une dérivée n ième
Bonjour, on peut remarquer que -u_{n+1}(x) = u_{n+1}(x)\left(x^{u_{n+1}(x)-u_n(x)}-1\right)) , qui permet d'obtenir un équivalent par récurrence.
, qui permet d'obtenir un équivalent par récurrence.
- 20 Aoû 2021, 16:45
- Forum: ✯✎ Supérieur
- Sujet: Une dérivée n ième
- Réponses: 11
- Vues: 800
Re: Dénombrement
Les coloriages en noir et blanc avec maximum k-1 cases noires alignées fournissent des coloriages à N(k-1)+1 couleurs pour le problème de départ. Avec N = 7 et k = 5 ça donne 29 couleurs. Comme N est premier on ne peut pas tricher avec une macro-grille régulière, mais en fait on peut toujours appliq...
- 17 Aoû 2021, 16:12
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 25
- Vues: 1717
Re: Dénombrement
En ce qui concerne "ma" méthode, le fait qu'on ne peut pas mettre strictement plus de 120 cases noires dans une grille 20x20 sous contrainte que chaque/ligne colonne a au plus 6 cases noires découle de l'argument utilisé plus tôt dans le thread pour obtenir un majorant (20 lignes, maximum ...
- 17 Aoû 2021, 13:47
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 25
- Vues: 1717
Re: Dénombrement
Une nouvelle tentative, à 121 couleurs cette fois (4 carrés 5x5 sur la diagonale + 4 morceaux de sous-diagonales de 5 cases chacun). On peut peut-être encore se rapprocher de 140 (voire l'atteindre ?) https://nsa40.casimages.com/img/2021/08/16/210816072934317077.png Si on admet que le problème qui c...
- 16 Aoû 2021, 18:19
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 25
- Vues: 1717
Re: Dénombrement
Je vois déjà que je me suis trompé dans une simple addition, mon coloriage fait 113 couleurs et non 117, ça m'apprendra à taper des calculs simples avec mes doigts maladroits. En espérant qu'il n'y ait aucune autre erreur, on découpe 3 carrés 6x6 et 1 carré 2x2 sur la diagonale. On colorie temporair...
- 16 Aoû 2021, 15:15
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 25
- Vues: 1717
Re: Dénombrement
Bonjour, je n'ai pas non plus la solution, mais comme lyceen95 j'ai l'impression que 140 est un majorant impossible à atteindre. En tout cas je ne vois pas comment on pourrait colorier chaque ligne en utilisant 7 nouvelles couleurs : une fois arrivé à la 8ème ligne on ne pourra pas respecter la cont...
- 16 Aoû 2021, 13:53
- Forum: ✯✎ Supérieur
- Sujet: Dénombrement
- Réponses: 25
- Vues: 1717
Re: Convergence en proba
Bonjour, on peut montrer que l'espérance de T_n tend vers \frac{\mu}{1-\alpha} et que la variance de T_n tend vers 0 (en faisant attention au fait que, les X_k n'étant pas indépendantes, la variance de T_n ne fait pas seulement intervenir la somme des variances des X_k ). On devrait donc s'en sortir...
- 08 Juin 2021, 18:51
- Forum: ✯✎ Supérieur
- Sujet: Convergence en proba
- Réponses: 6
- Vues: 595
Re: Python: tracer une fonction complexe.
La courbe que tu cherchais à tracer est le graphe de la fonction réelle arcsin. Le fait que tu aies choisi d'écrire arcsin sous une forme qui fait intervenir des complexes ne change rien à l'affaire. Après tu peux tracer d'autres choses si tu veux, par exemple le segment de droite horizontal que tu ...
- 26 Mai 2021, 13:26
- Forum: ϟ Informatique
- Sujet: Python: tracer une fonction complexe.
- Réponses: 5
- Vues: 1449
Re: Restriction d'une distribution
Oui, et dans ce cas particulier je pense pas que l'abus soit bien grave. Sinon ça pourrait en effet valoir le coup de regarder si on peut définir un opérateur trace pour les distributions ou certaines d'entre elles. Dans mes souvenirs, la trace a besoin de vivre dans L^p donc ça ne me paraît comprom...
- 26 Mai 2021, 11:37
- Forum: ✯✎ Supérieur
- Sujet: Restriction d'une distribution
- Réponses: 3
- Vues: 600
Re: Python: tracer une fonction complexe.
Bonjour, de ce que je peux voir de ton code, tu es en train de tracer le graphe de Im(z) en fonction de Re(z), et tu obtiens quelque chose qui a l'air correct : z est censé être réel (c'est l'arcsinus d'un réel entre -1 et 1) donc le graphe que tu demandes de tracer est un segment de droite horizont...
- 25 Mai 2021, 19:18
- Forum: ϟ Informatique
- Sujet: Python: tracer une fonction complexe.
- Réponses: 5
- Vues: 1449
Re: Restriction d'une distribution
Bonjour, on peut restreindre les distributions à condition que le domaine de restriction soit un ouvert : partant d'un ouvert \Omega et d'une distribution f\in\mathcal{D}^\prime (\Omega) , on définit la restriction de f à un ouvert \omega \subset \Omega par \langle f_\omega , \phi\rangle = \...
- 18 Mai 2021, 13:16
- Forum: ✯✎ Supérieur
- Sujet: Restriction d'une distribution
- Réponses: 3
- Vues: 600
Re: Monde en 2D
Oui en effet, il faudrait sans doute rajouter un canal courbé dans la partie basse comme dans ton post précédent pour solidariser le tout ?
- 11 Mai 2021, 22:23
- Forum: ⚔ Défis et énigmes
- Sujet: Monde en 2D
- Réponses: 25
- Vues: 1602
Re: Monde en 2D
Bonjour, l'exercice a l'air très intéressant donc j'y ai réfléchi un peu. Une modeste contribution pour la passoire (un piston, en fait) en piquant la liaison pivot proposée par GaBuZoMeu (mais a priori on devrait pouvoir faire une version plus avancée avec la liaison en spirale de Vassillia). Il n'...
- 11 Mai 2021, 17:09
- Forum: ⚔ Défis et énigmes
- Sujet: Monde en 2D
- Réponses: 25
- Vues: 1602
Re: Solution des EDP linéaires homogènes
Les parties réelles et imaginaires des ^n) engendrent toutes les solutions polynomiales, si ma mémoire ne me fait pas défaut.
engendrent toutes les solutions polynomiales, si ma mémoire ne me fait pas défaut.
- 17 Fév 2021, 00:26
- Forum: ✯✎ Supérieur
- Sujet: Solution des EDP linéaires homogènes
- Réponses: 4
- Vues: 727
Re: Solution des EDP linéaires homogènes
Bonjour, Une réponse quelque peu tardive : intuitivement, à partir du moment où on a affaire à des EDP, les conditions initiales et/ou aux limites qui correspondent aux degrés de liberté des solutions ne sont plus des nombres mais des fonctions. Du coup, dans les cas génériques il y a fort à parier ...
- 15 Fév 2021, 16:08
- Forum: ✯✎ Supérieur
- Sujet: Solution des EDP linéaires homogènes
- Réponses: 4
- Vues: 727
Re: stabilité espace caractéristique
Bonjour,
^m) est un polynôme en u, qui commute donc avec u.
est un polynôme en u, qui commute donc avec u.
- 11 Juil 2020, 18:27
- Forum: ✯✎ Supérieur
- Sujet: stabilité espace caractéristique
- Réponses: 3
- Vues: 1070
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
