Complexité : simplifier et dominer une somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par PythagoreSauvage » 09 Mar 2022, 10:11
par PythagoreSauvage » 09 Mar 2022, 10:11
Bonjour à tous, je suis en train de calculer la complexité d'un algorithme et je tombe sur une somme, que je n'arrive pas à simplifier, et dont j'essaye d'extraire un
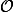
:
Soit
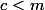
. J'ai la somme suivante :
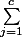
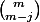
^2)
que je n'arrive pas à dominer/majorer
Si quelqu'un à une idée,
D'avance merci
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 09 Mar 2022, 13:44
par tournesol » 09 Mar 2022, 13:44
La majoration
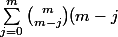^2)
est calculable.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 09 Mar 2022, 14:11
par tournesol » 09 Mar 2022, 14:11
Ma réponse précédente est égale à
2^{m-2})
qui est un
)
 par PythagoreSauvage » 09 Mar 2022, 14:55
par PythagoreSauvage » 09 Mar 2022, 14:55
AH oui c'est tout à fait exact, je ne sais pas si c'est pas trop brutal comme majoration mais à mon avis c'est la manière la plus simple je dirais, ou la seule qui permet d'avoir un résultat exploitable
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 09 Mar 2022, 15:22
par Skullkid » 09 Mar 2022, 15:22
Bonjour, on peut également majorer crûment par
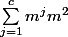
qui donne du
)
. Ça donne une meilleure borne pour les petites valeurs de c.
 par PythagoreSauvage » 09 Mar 2022, 15:49
par PythagoreSauvage » 09 Mar 2022, 15:49
AH oui pas mal merci Skullkid, d'autant qu'on a une borne sur c en fait (qui dépend d'un autre paramètre k < m, on sait que c <= (m-k)/2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités